Last Updated: 06/03/2020
What is Bootstrapping?
Bootstrapping is any test or metric that uses random sampling with replacement. In time series, block bootstrapping is commonly used to capture structural dependency. Three block bootstrapping methods are introduced.
- Moving Block Bootstrap: Data is split into n − b + 1 overlapping blocks of length b: Observation 1 to b will be block 1, observation 2 to b + 1 will be block 2, etc. Then from these n − b + 1 blocks, n/b blocks will be drawn at random with replacement. Then aligning these n/b blocks in the order they were picked, will give the bootstrap observations.[1] This bootstrap works with dependent data, however, the bootstrapped observations will not be stationary anymore by construction
- Stationary Bootstrap: Stationary bootstrap is a modification of Moving Block Bootstrap. By varying randomly the block length can avoid the problem of construction of nonstationary observations mentioned above.[30]
- Circular Bootstrap: Coming soon
Use Case
We use Bootstrapping for Univariate time series forecasting.
What will you build?
- Different Bootstrapping methods for generating synthetic univariate time series data.
What will you learn?
- Preprocessing required for generation of synthetic time series
- How to use various bootstrapping methods
- How to analyse various generated scenarios
Getting Data
We can fetch the data in 2 possible ways:
- From FRED datasource (Learn more here)
- Uploading .csv file
The data has values (prices, indexes etc.) and corresponding timestamp.
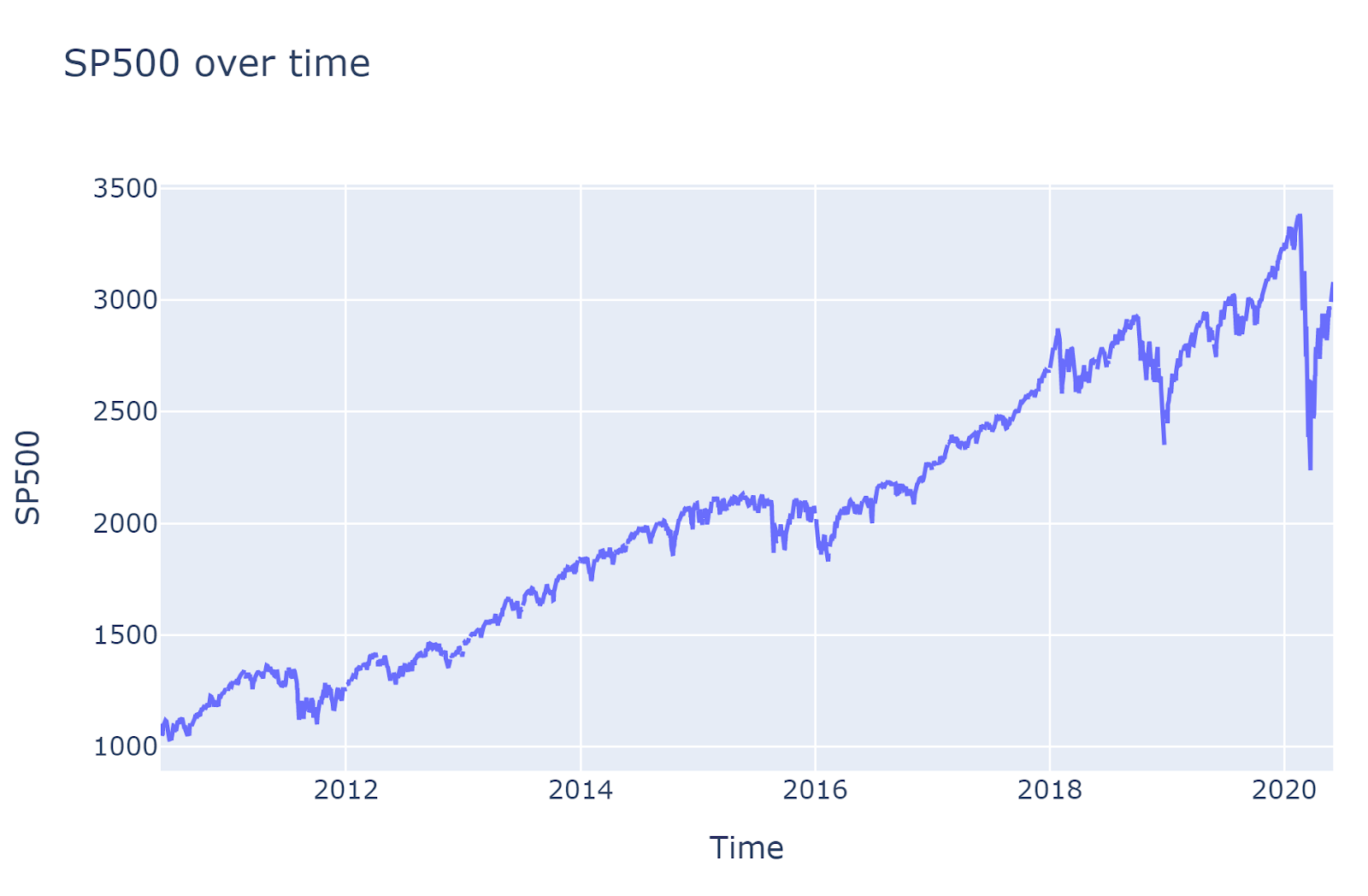
Restructuring data for ingestion
Since Bootstrapping works with stationary data, and price values are not stationary. It is necessary to convert price into return.
The data is automatically converted from its original values 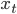 into returns
into returns 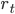 .
.

Apart from this, this section also provides functionality for clipping the data between start_date and end_date.
And users can choose one of the three bootstrapping methods above.
| Training Start and End date can be used to clip the dataset as per the usage. Forecasting Horizon Forecast period specifies how much in future you want to forecast, determined by Start and End date. |
| Model Parameters[3]
|
About model
The model comprises an three components:
- Stationary Bootstrap
- Block size is a random number following exponential distribution with mean value equal to 4.
Model Result
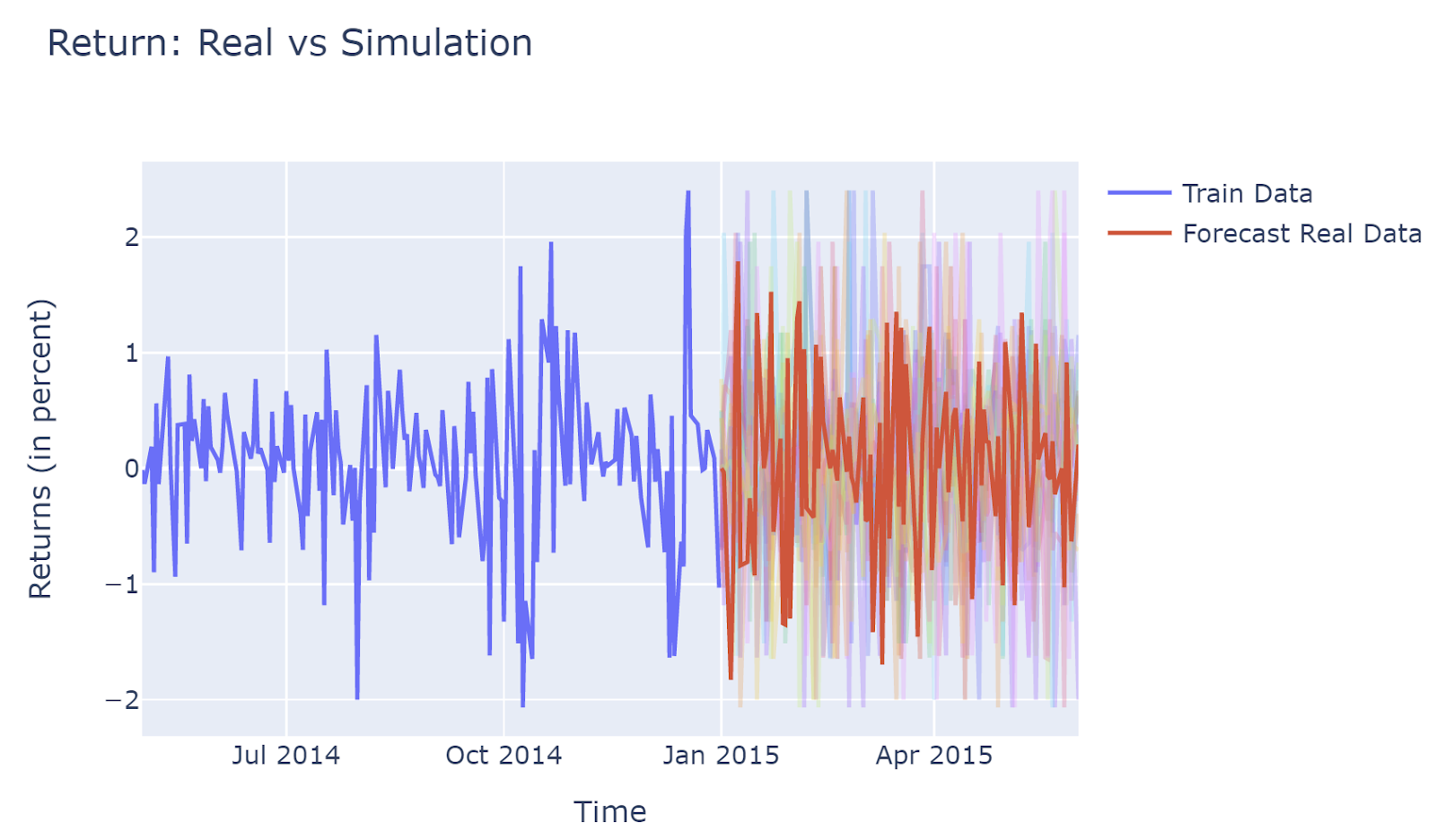
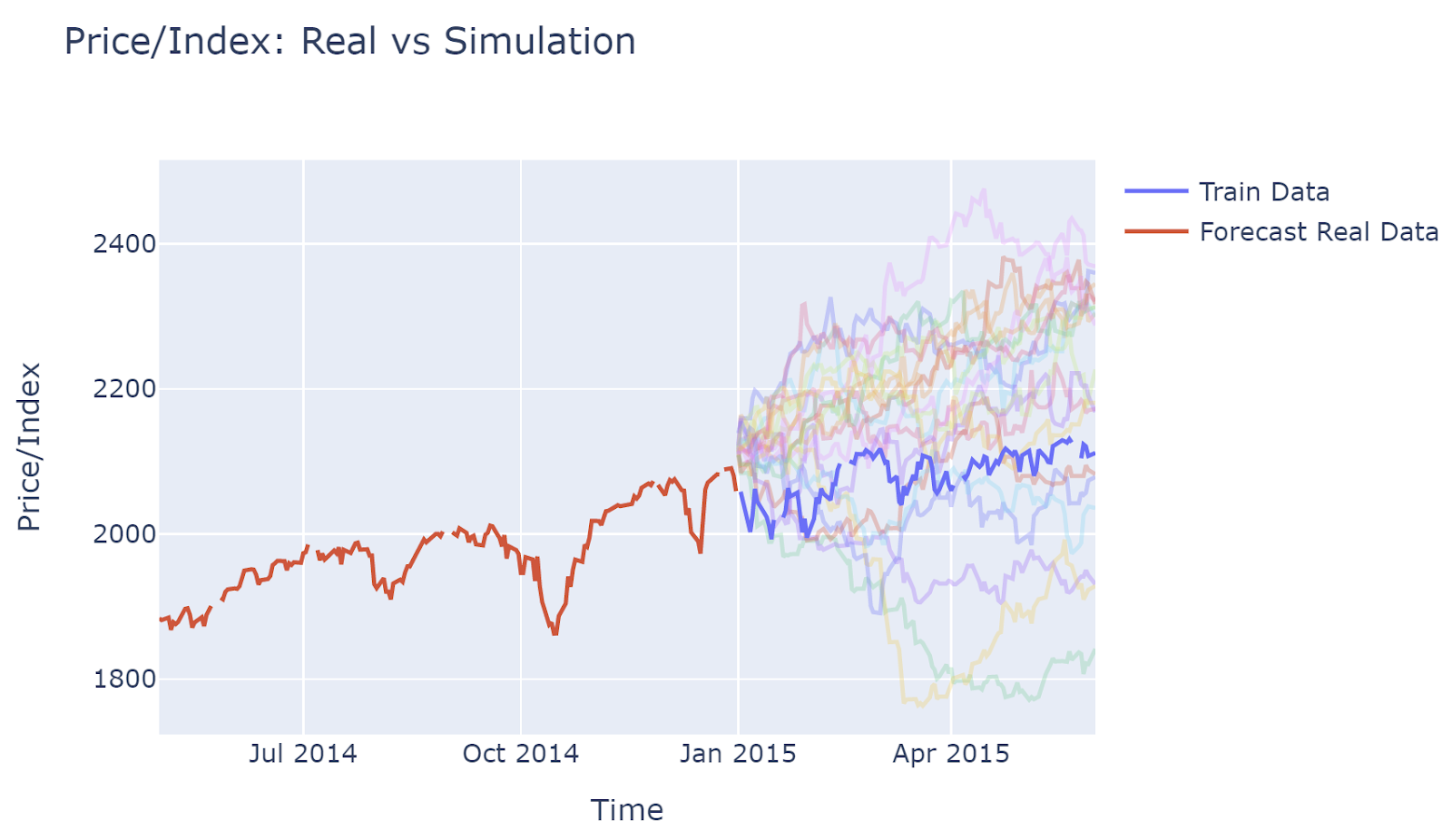
The graph of price, which is converted back from returns, shows that most simulations capture the uptrending of stock movement. This is due to the historical data showing an upward trend, and bootstrapping method taking historical data would also show upward trending.
This section includes analysis over simulation data, and divided into the following subsections:
- Simulation Samples
- Histogram/Distribution of observations at a single timestep, t (t=0 by default)
- Distributions of entire forecasting periods, represented by mean and standard deviation
- K-Means Clustering of Scenarios
- Hierarchical Clustering of scenarios
- Clustering Comparison
- Discriminative Score(coming soon)
- Predictive Score(coming soon)
- PCA(coming soon)
- tSNE(coming soon)
| Simulations specify if you want to apply the following analysis over return or price. |
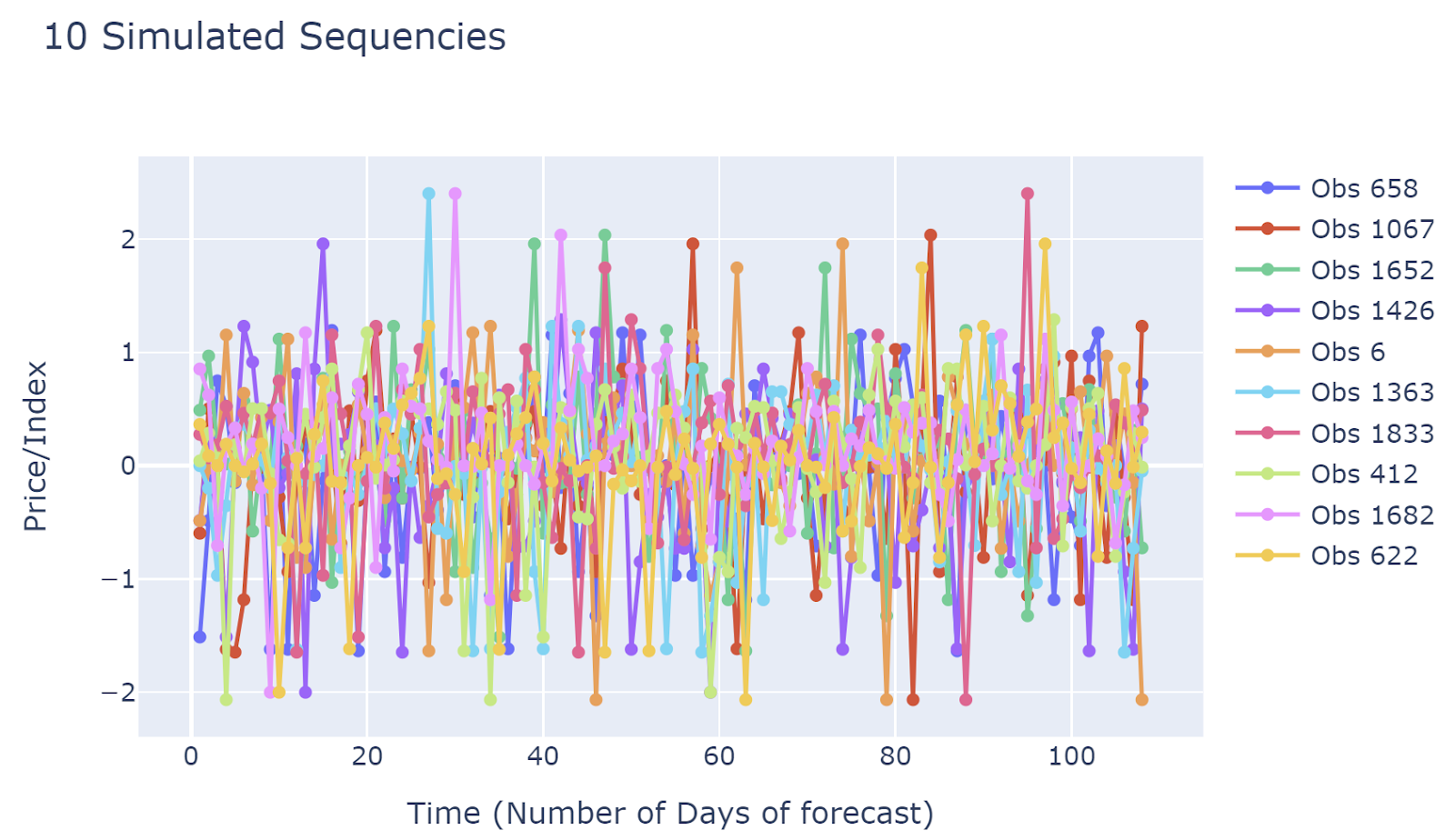
Simulation Samples
Take a look at some randomly selected simulations.Simulated results are quite different from each other. This implied that the simulation results may capture many different scenarios. The disadvantage would be due to the large number of simulated sequences, it is hard to have generalized insights.
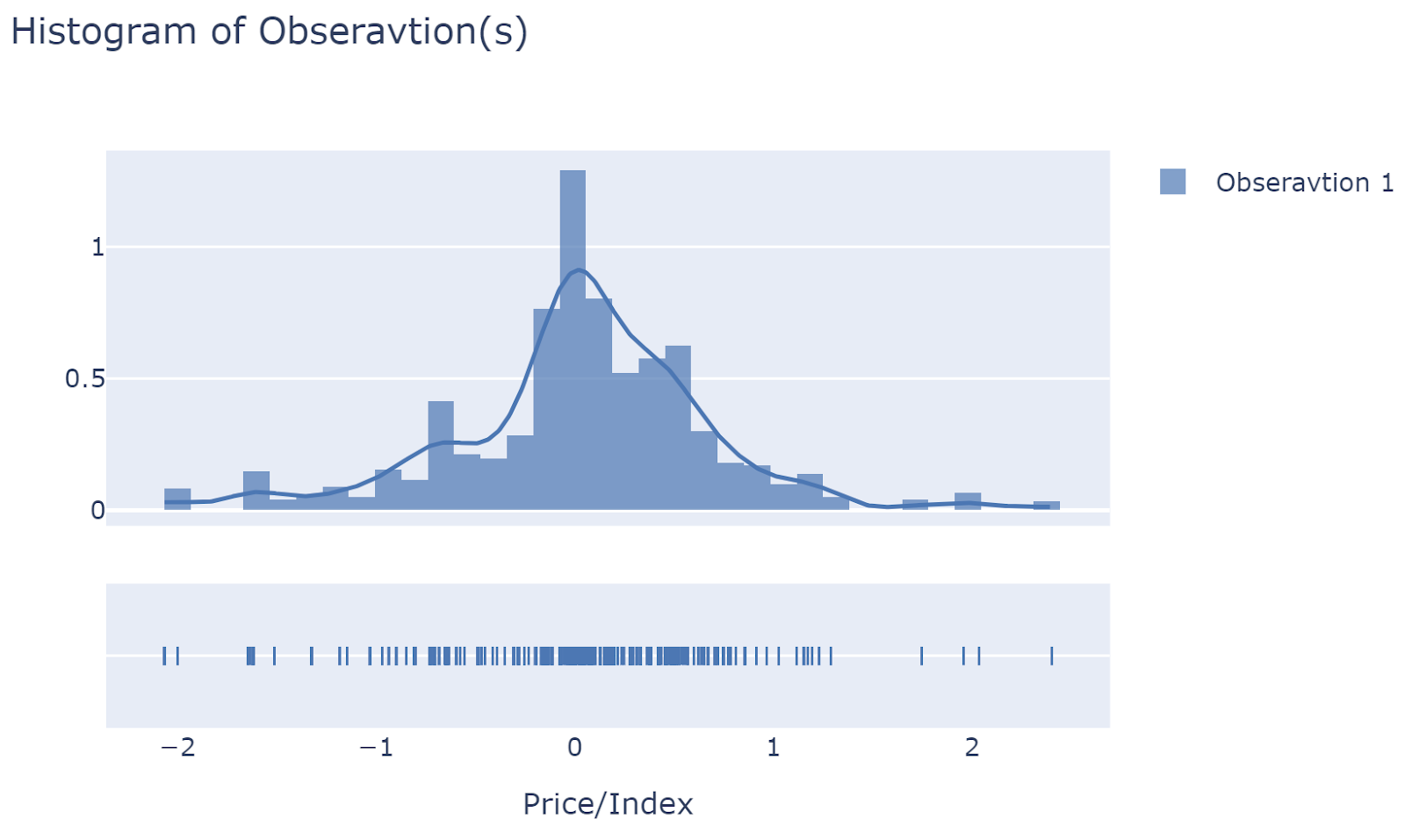
Histogram/Distribution of observations at a single timestep
It is recommended to plot the histogram of the first time point. If it is distributed around the latest realized value (prices/index), then at least we can say that simulated data is not unrealistic.
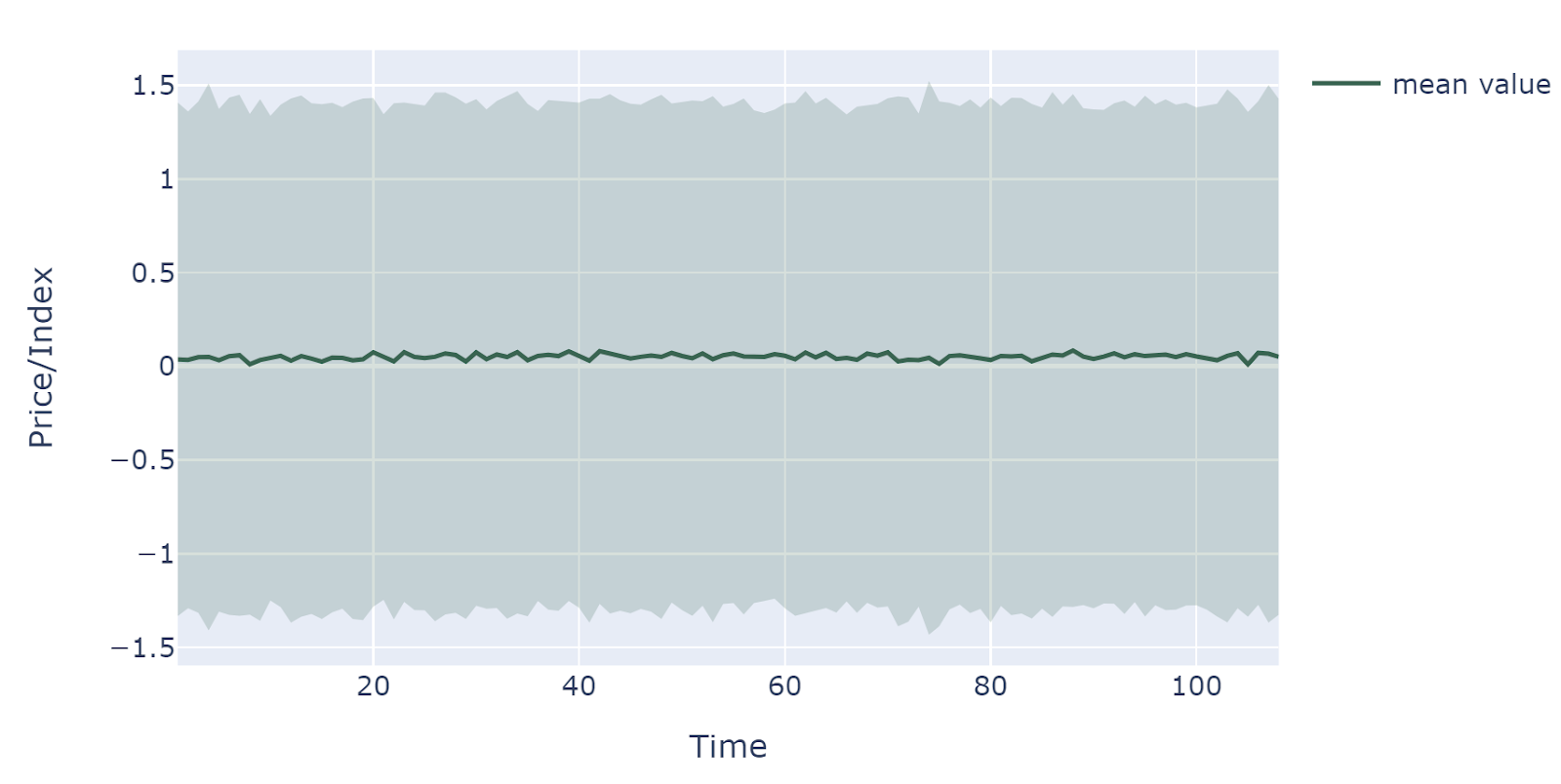
Distributions of entire forecasting periods
The middle line is the mean value of all simulations while the filled area is determined by the standard deviation of simulations at each time step. Due to bootstrapping is in nature a random copy of historical data and thus the expected value and variance of simulation would be consistent overtime.
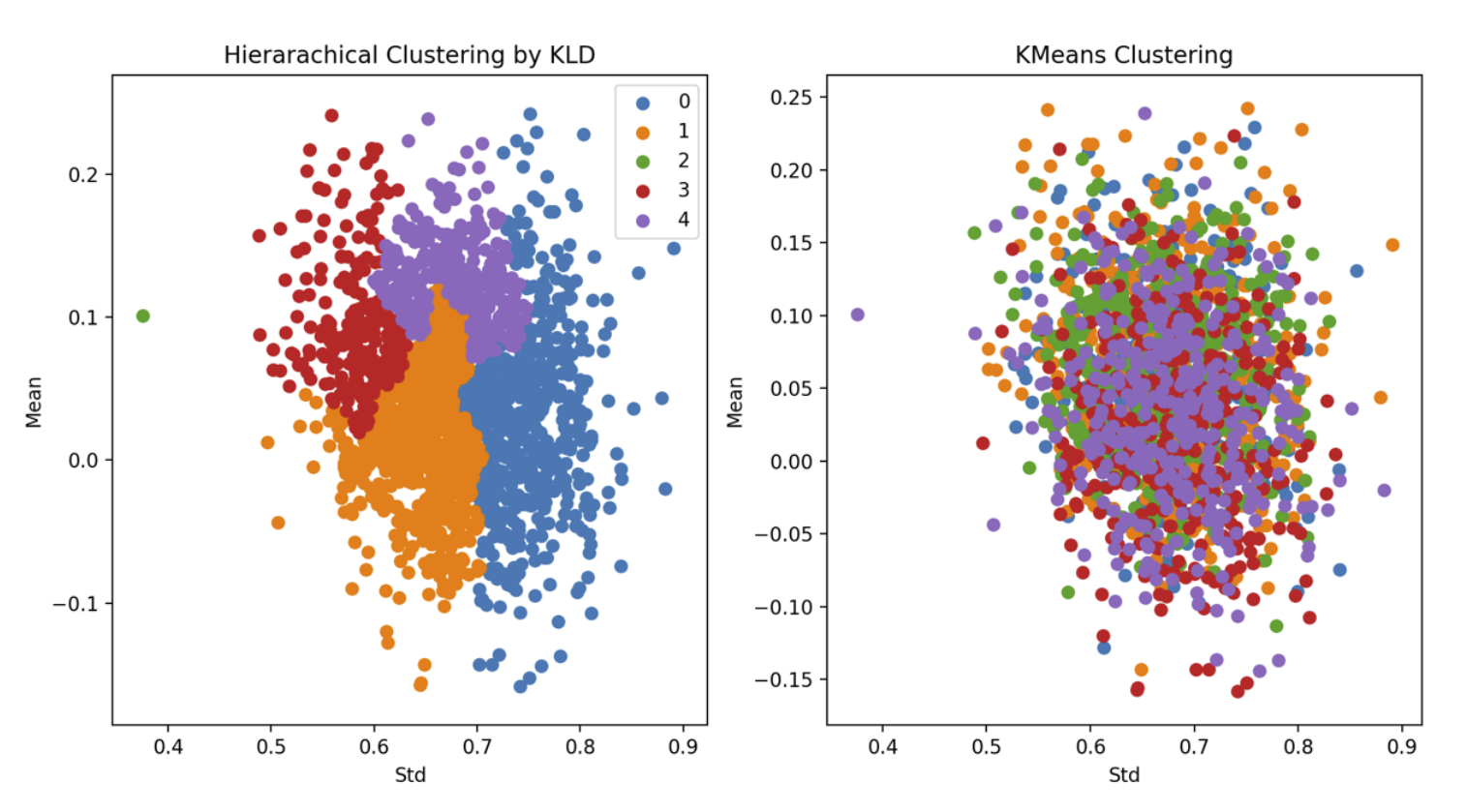
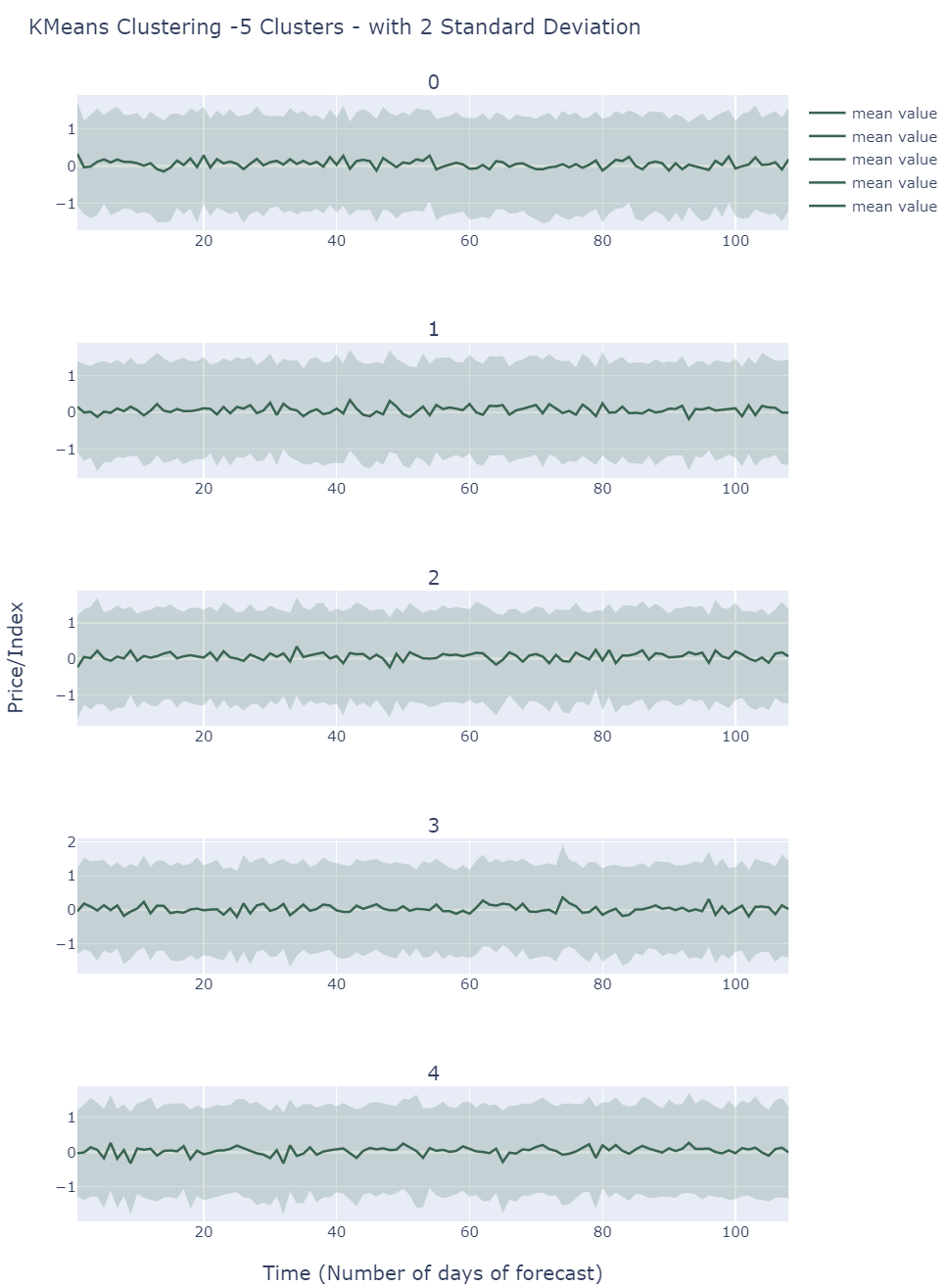
K-Means Clustering of Scenarios
By default , we choose 5 clusters using L2-K-Means clustering to extract different scenarios. Other than cluster 3, the other clusters are almost the same in terms of variance and mean value. Even cluster 3 is only a bit more volatile. The reason is that all of the 5 clusters follow the same distribution and show present similar behaviour.
Hierarchical Clustering of scenarios
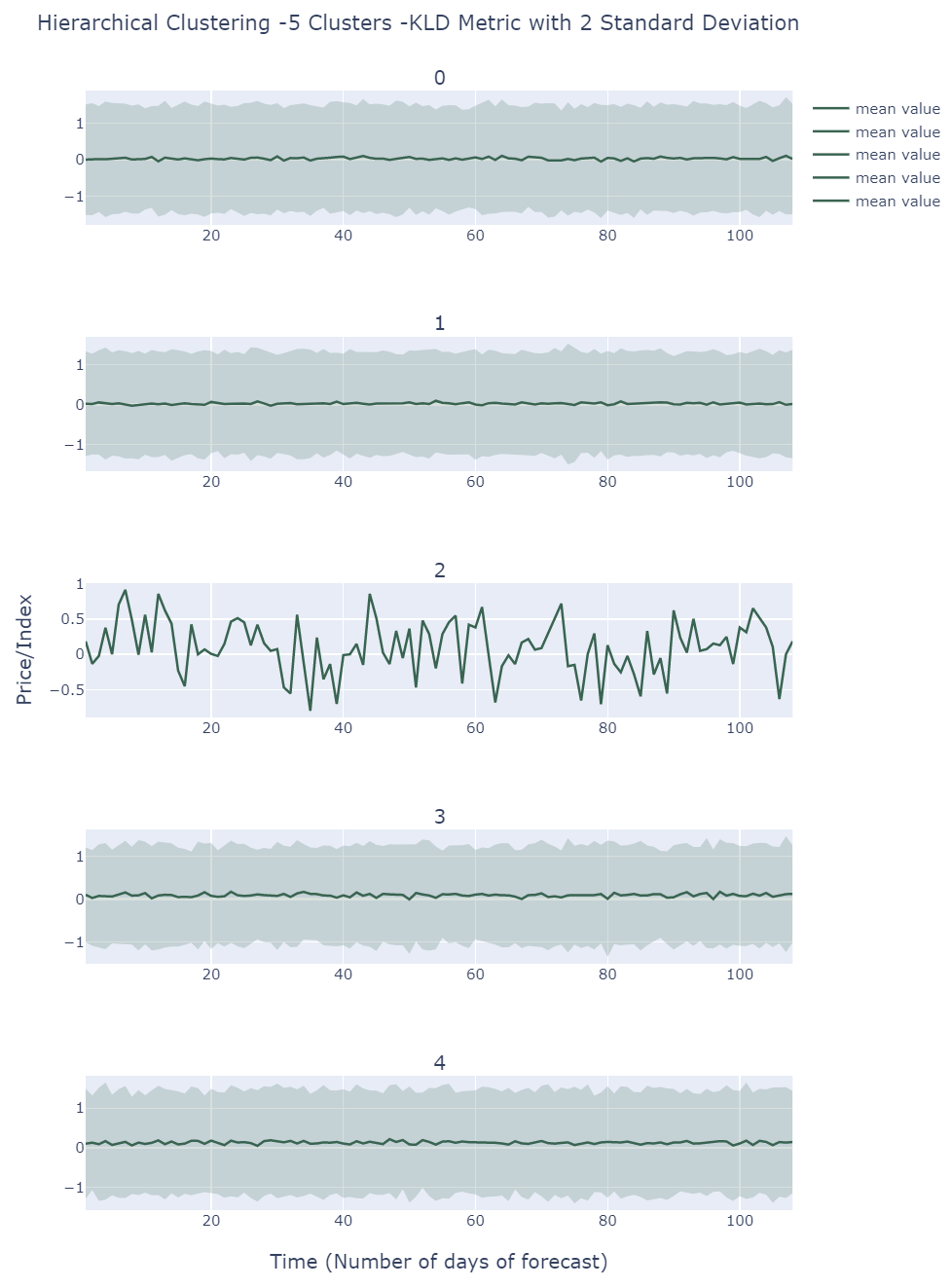
By default , we choose 5 clusters using Hierarchical Clustering(KL Divergence Affinity) to extract different scenarios. The same conclusion from KMeans also applies here. The only difference is that Hierarchical Clustering tends to throw away one outlier instead of a group of outliers.
 .
.
Clustering Comparison
Clustering is a method allowing us to focus on major patterns reflected by the simulation. KMeans seems only able to identify outliers, almost impossible situations but KLD Hierarchical Clustering is able to separate scenarios based on the volatility imply stable and a little less stable future is most likely to happen.