Description of the problem
Lending Club strives to connect borrowers with investors through our online marketplace.
The goal is to predict the interest rates that Lending Club should use, based on previous borrowers data they have. Whether or not a client will repay a loan or have difficulty is a critical business need. In this project, we are going to see some models that the machine learning community can develop to help organizations like Lending Club.
What you will build
- A neural network with tuned hyperparameters.
What you will learn
- Module 3: Hyperparameters tuning
The experimentation will be done in Jupyter Notebooks, primarily in Python3.6.
- pandas
- numpy
- matplotlib
- seaborn
- scipy
- sklearn
In this project, we are going to use the Lending Club loan dataset. The provided file is a cleaned version of the original Lending Club dataset available at Kaggle. The files provided includes a file containing the description of the features, LCDataDictionary, and the data file named LendingClubLoan.csv.
The original version of the dataset is about 230mb. The version provided is a subset of 9999 samples of the cleaned dataset. Let us first take a look at some of the features in the given dataset. The entire list can be found in the jupyter notebook.
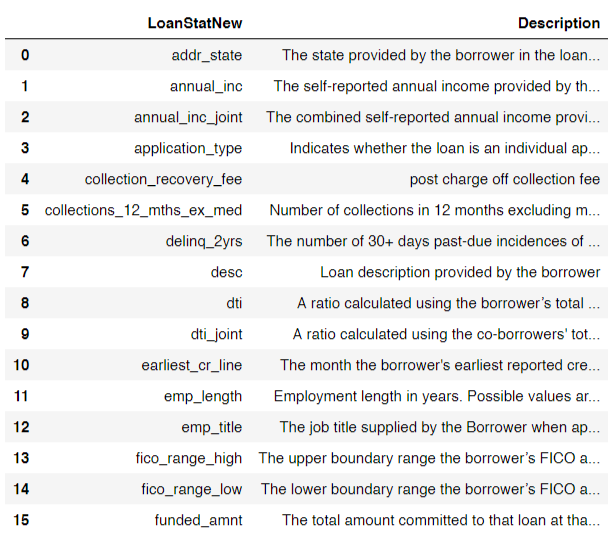
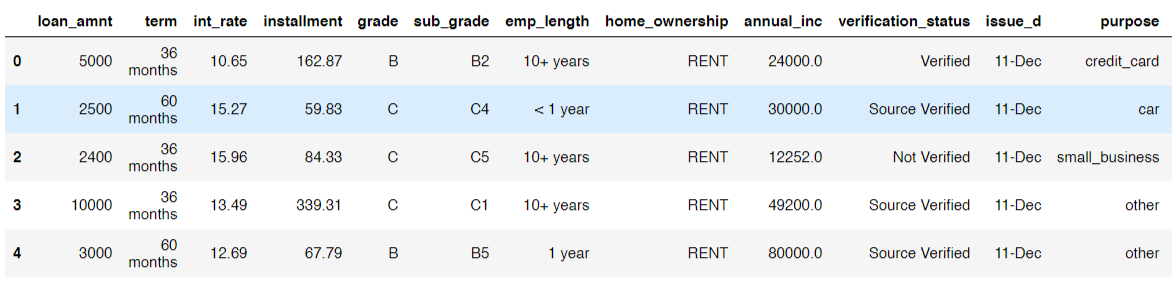
Here is a look at some of the entries in the dataset:
Most of the machine learning models can be (vaguely) considered as a non linear mathematical function with many parameters, which are called weights in the case of a neural network.
Parameters of a neural network are the weights associated with the neurons that are actually involved in the calculations. Hyperparameters on the other hand are factors that determine how the model will be trained, like the number of iterations, the algorithms to be used, penalties to be applied and so on. These are the parameters that have to be decided by the quant/data scientist making the model.
Neural networks have a lot of hyperparameters that show their immediate effects on the learning curve, so we will choose this as a means to study hyperparameters.¶
Artificial neural networks (ANN) are computing systems vaguely inspired by the biological neural networks that constitute animal brains. Such systems "learn" to perform tasks by considering examples, generally without being programmed with any task-specific rules.
Neural networks can be used as classification models as well as regression(prediction) models.
Perceptron
A perceptron is a linear classifier, that can classify linearly separable data.
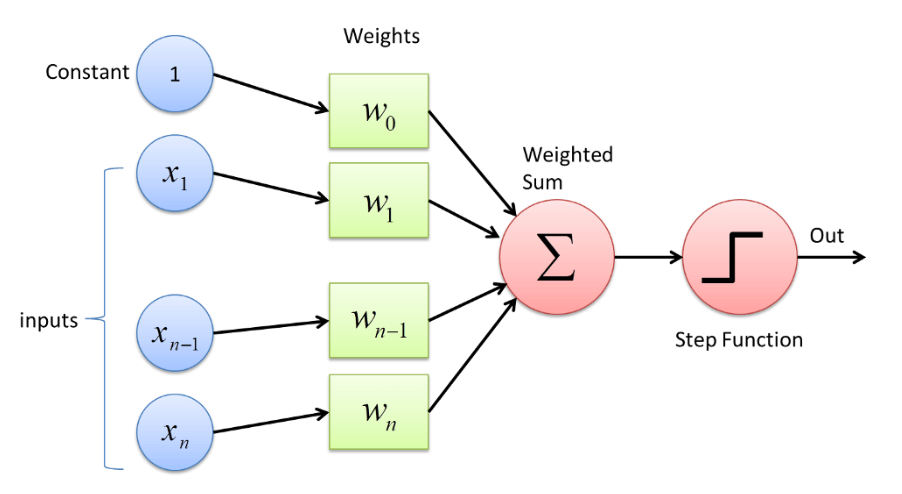
A multilayer perceptron is called as a neural network. It is a combination of many linear classifiers that enables it to fit to non linearly separable data. The features are the inputs of the neural network. The circles here represent neurons in the neural network, each with its own weights (coefficients).
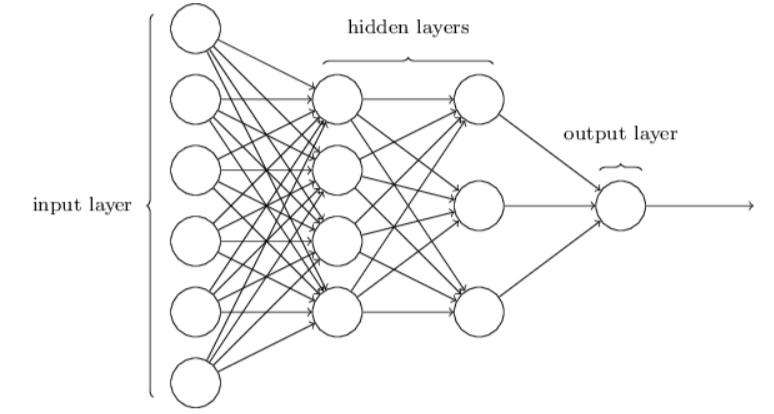
Layers, Weights, and Backpropagation in Neural Networks
For our data set, the number of features are 16. Each layer between the input layer (where we enter the dataset) and output layer (where we obtain our predicted value) is called as a hidden layer of the neural network. Usually, but not always, higher number of layers tend to capture more nuances in the data and fit the training data better.
When we pass in the labels(y) and the features(X) to a training model, the weights in these layers act as coefficients and multiply the value of the feature and ultimately gives out a single value (can be multi-dimensional output as well) at the output layer.
This value is checked against the actual value or label that we pass, the difference in the actual and predicted value gives us a loss. This loss is then distributed back in all the layers to accommodate for it. This is done using various algorithms, most prominently back propagation algorithm. The rate at which these changes occur can be regarded as learning rate.
You can also think of a neural networks loss function as a surface, where each direction you can move in represents the value of a weight. Gradient descent is like taking leaps in the current direction of the slope, and the learning rate is like the length of the leap you take.
The learning rate tells the gradient descent how much to move in that direction.
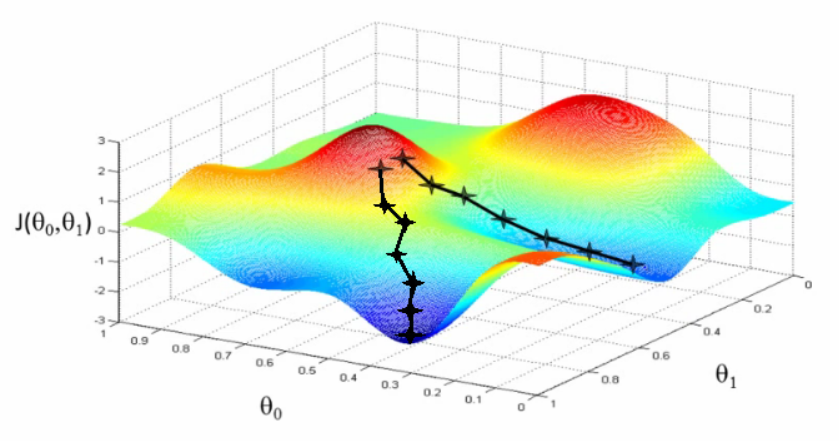
At really small rates and really large rates the optimization function may not converge at a minia.
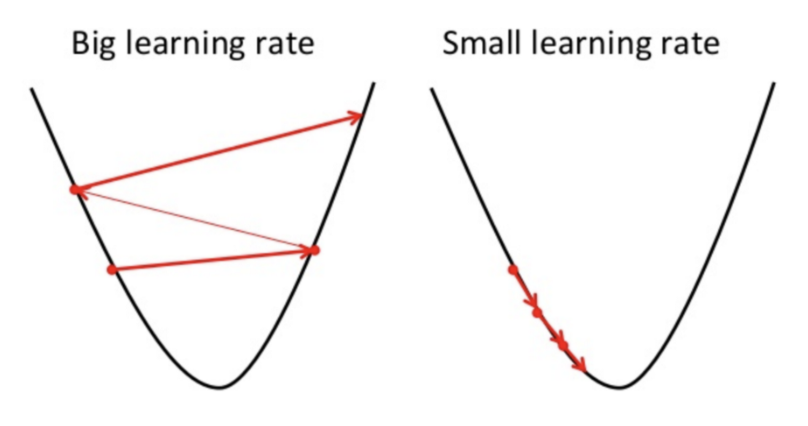
Experimentation
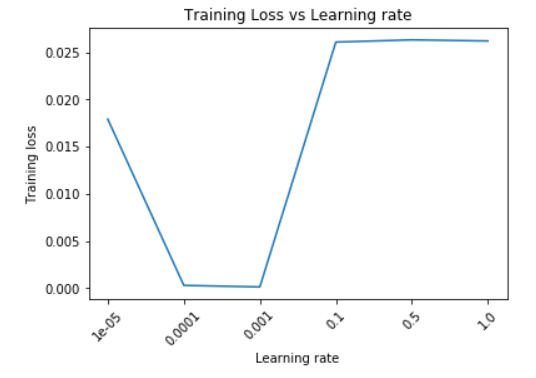
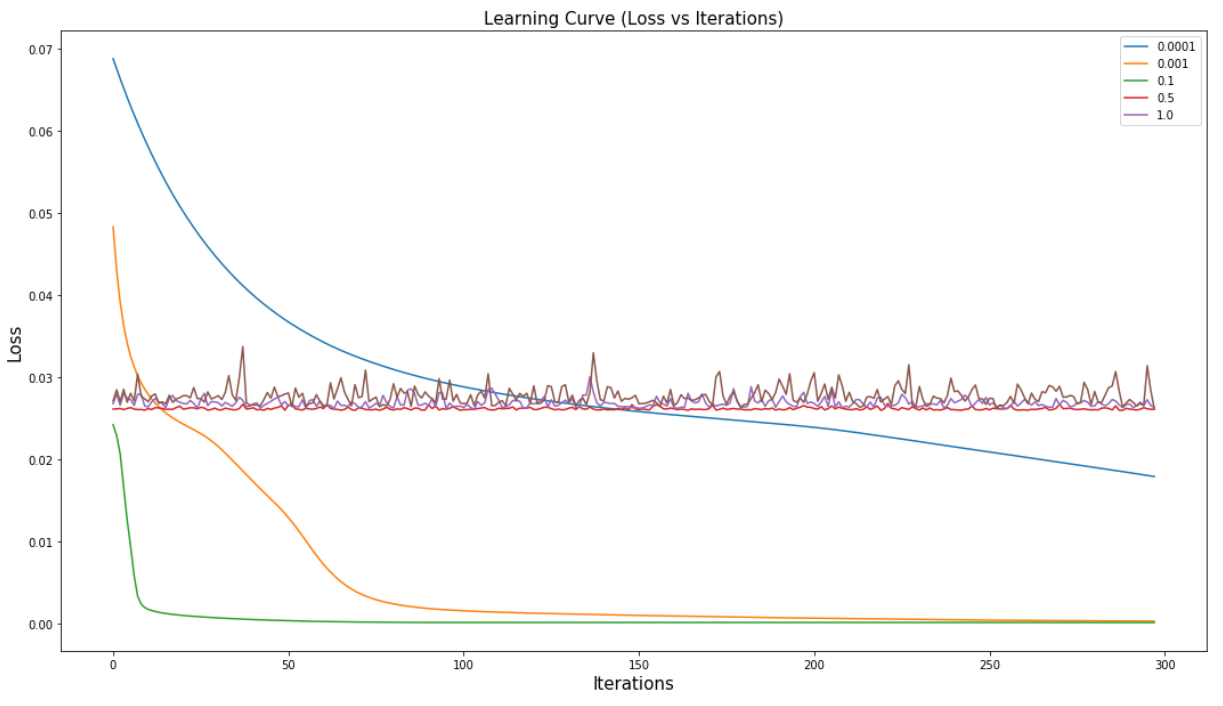
We run our neural network model on several learning rates, keeping all other hyperparameters same.
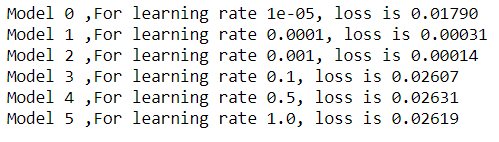
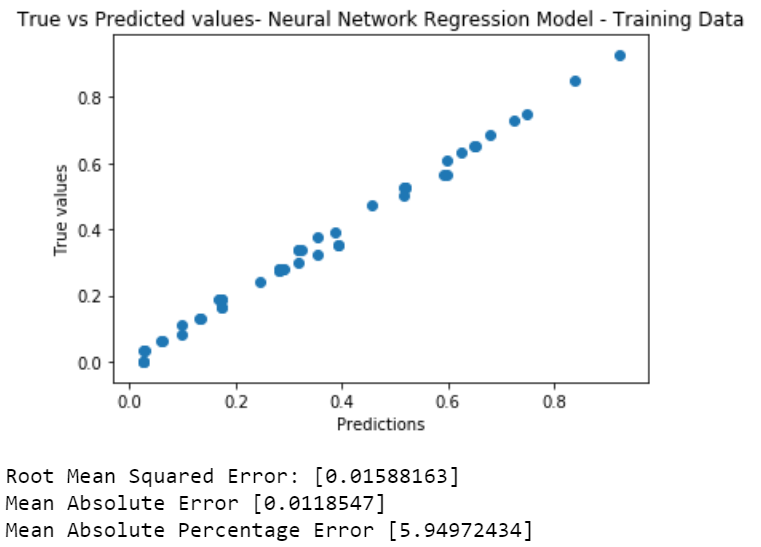
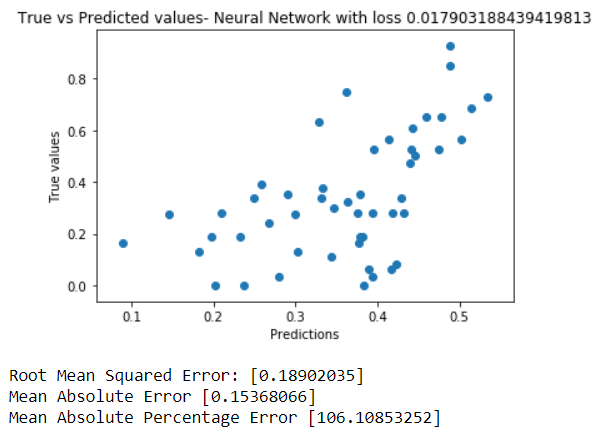
The graph of true values vs predictions show no trends at all. This means that the predicted values are nowhere related to the true values. For a really low learning rate, there wasn't any considerable learning in 300 iterations. This is due to really small learning rate of 0.00001, so the function could not find a minima.
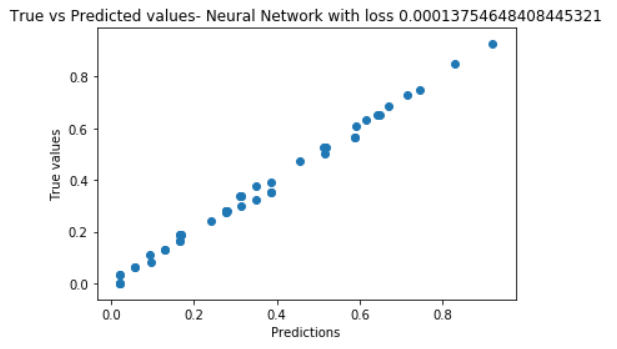
The graph of true values vs predictions lie on a line with slope of around 45 degrees. This means that the predicted values are almost same as the true values. Had they been identical, we would have seen a single line at 45 degree. For a learning rate of 0.01 the loss is considerably low.
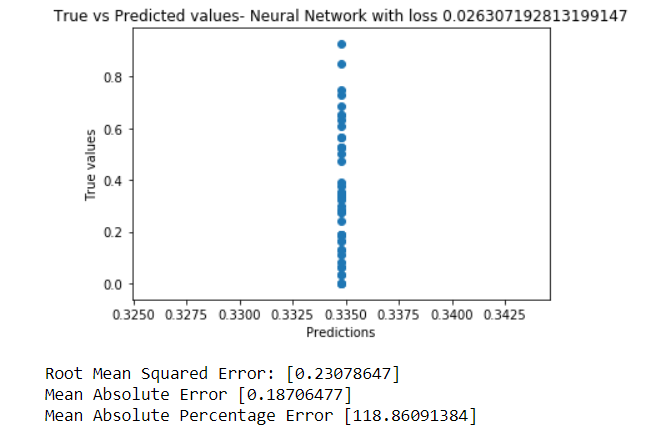
The graph of true values vs predictions lie on a straight vertical line. This means that the model just predicted a single value for all inputs. This is a result of very very high learning rate of 0.5. Due to high rate, the gradient descent missed and overshot the minima.
At high learning rates, the learning curve does not show any improvement, at low rates, there is very gradual improvement, and at the optimal value of bout 0.001 the convergence is good.
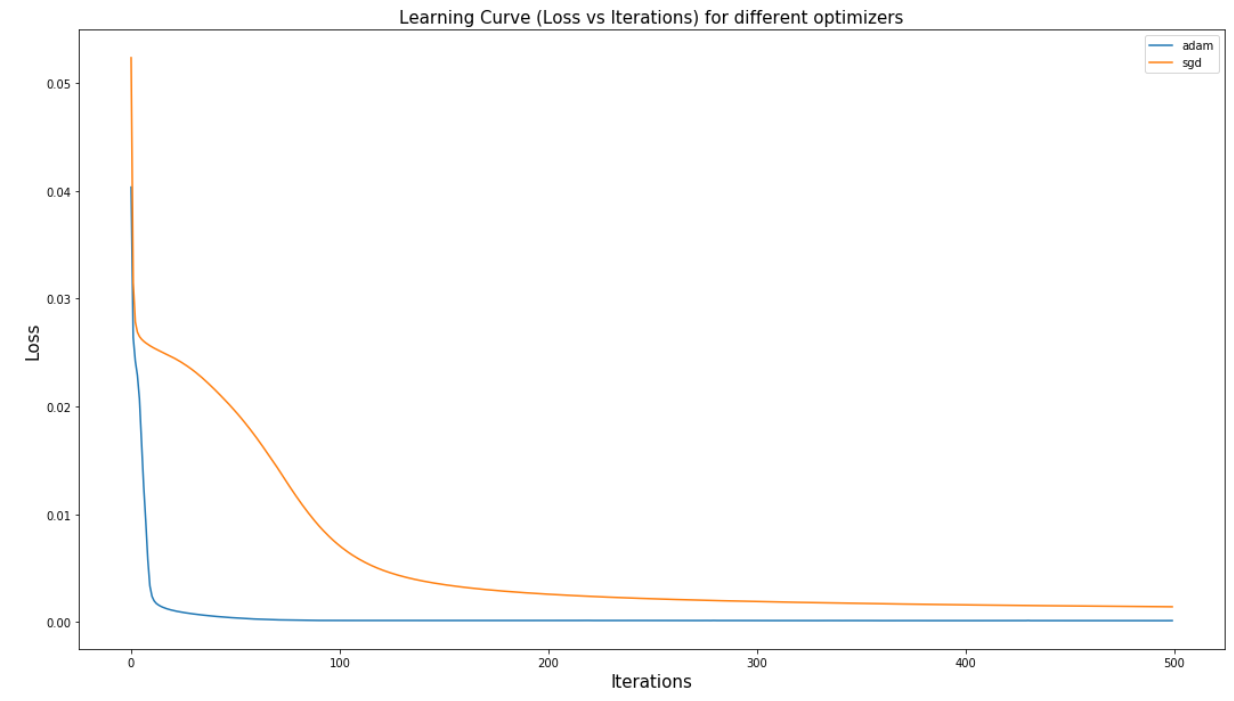
Now that we have selected the learning rate that yields lowest loss, let us see what effect does the optimization algorithm have on the model.
An optimization algorithm is a procedure which is executed iteratively by comparing various solutions till an optimum or a satisfactory solution is found. Neural networks use various optimization algorithms to back propagate the losses.
A few of the prominent ones provided by scikit-learn package iare Adam optimizer and SGD (Stochastic Gradient Descent).
Experimentation

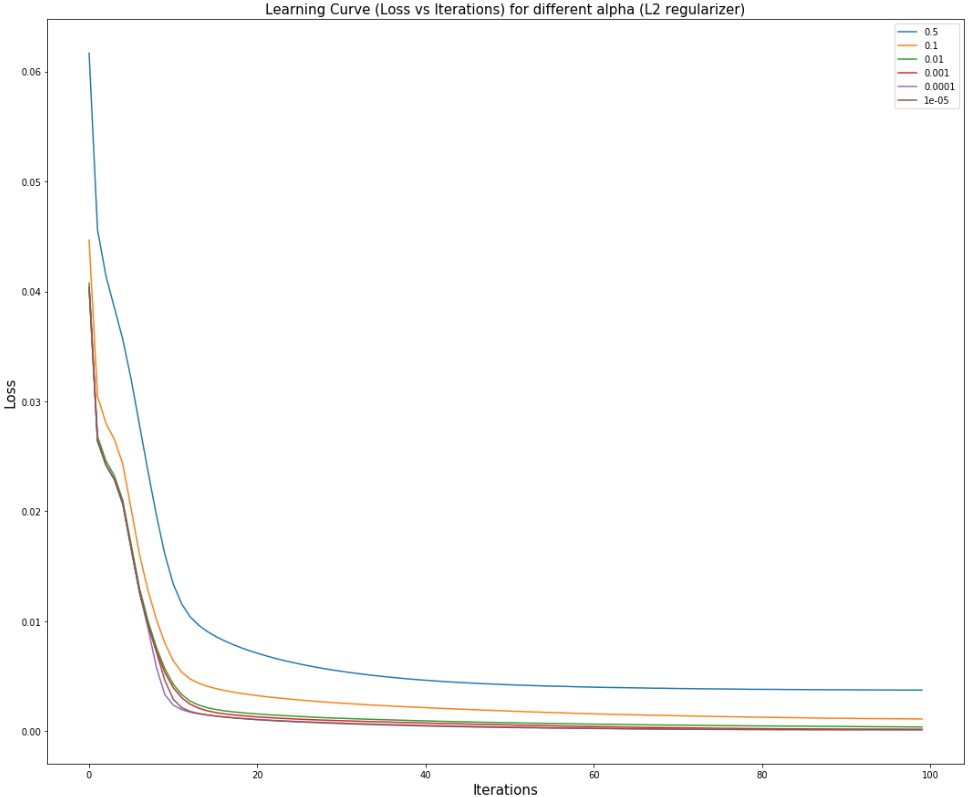
Regularization basically adds a penalty as model complexity increases. Regularization parameter (L2 alpha) penalizes all the parameters except intercept so that model generalizes the data and won't overfit and the parameters are not updated as drastically.
Overfitting and Underfitting
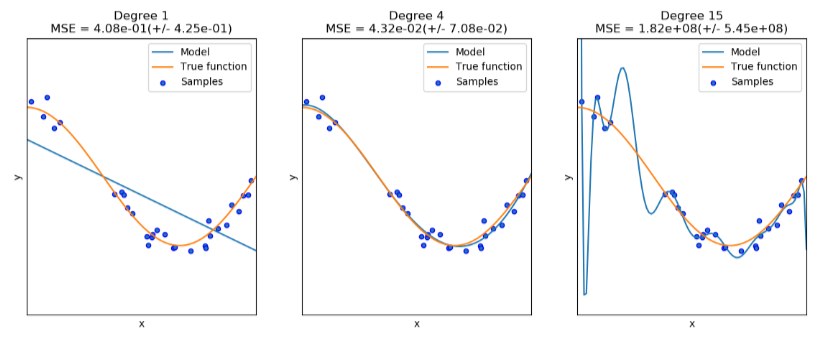
Overfitting refers to the fact that the model has fit the training data so well that it doesn't recognise outliers i.e. it has fit the noise in the training data as we. A more complex model usually tends to overfit. For example, a neural net with too many layers may fit to the training data very well but wont be able to generalize on testing or validation data set.
Overfitting causes the model to not accept new samples readily, i.e, it doesn't generalize well while making predictions.
Similarly there is underfitting, when the model is not able to provide a low loss even on the training data, let alone a testing dataset.
The first figure shows a sample of underfitting, the second one is a good fit and the third one is overfitting. A higher degree polynomial is more complex than a linear model in the first case, hence it overfits.
Experimentation
alpha - L2 regularizer value

High L2 penalty causes underfitting as it does not allow the model to train. So the L2 alpha values have to be low.
Activation functions are functions that introduce non linearities in the neural network. If we do not apply any non linearly, our entire network would be just one big linear function, only transforming the input from one layer to another.
A Neural Network without Activation function would simply be a Linear regression Model, which has limited power as we already saw in the last lab. We want our Neural Network to not just learn and compute a linear function but something more complicated than that.
ReLU or Rectified Linear Unit is the activation function we are using.
Mathematically: A(x) = max(0,x)
The configuration of the neural network is referred to as its architecture. The architecture for our network is as follows