Description of the problem

This project is designed to help you better understand linear optimization and to practice creating and solving linear optimization problems. This exercise uses Scipy in Python to manage shares of stocks of an investor.

Managing your portfolio is not an easy task. When you sell a stock, you have to pay both a transaction fee and tax on the money you gain. Sometimes you have to decide which stocks and how much you want to sell for, making sure you have enough cash for other purchases. In this problem, we will use linear optimization to decide which shares of stock and how many you need to sell in order to have enough cash to make your purchase and to maintain a strong portfolio of stocks.

Suppose that, last year, you purchased 150 shares of eight different stocks, for a total of 1,200 shares. The table below lists the stocks that you purchased, the price you purchased them for last year, the current price, and the price estimate for next year.

If you sell any shares, you have to pay a transaction cost of 1% of the amount transacted. In addition, you must pay capital-gains tax at the rate of 30% on any capital gains at the time of the sale. For example, suppose that you sell 100 shares of a stock today at $50 per share, which you originally purchased for $30 per share. You would receive $5,000. However, you would have to pay capital-gains taxes of 0.30 * ($5,000 - $3,000) = $ 600, and you would have to pay $50 in transaction costs (1% of $ 5,000). Therefore, by selling 100 shares of this stock, you would have a net cash flow of $5,000 - $600 - $50 = $4,350.

Note that for this problem, none of the stocks decreased in value since the time of purchase, so we do not have to deal with capital losses.

Here are the details of the situation:

• Last year, you purchased 150 shares of eight different stocks, for a total of 1,200 shares.
• The table below lists the stocks that you purchased, the price you purchased them for last year, the current price, and the price estimate for next year.
• Transaction cost = 1% of the amount transacted.
• Capital-Gains tax rate = 30%

Your aim is to sell enough shares of stock today to generate $10,000 to use as part of a down payment on a new home. You need to decide how many shares of which stocks to sell in order to generate $10,000, after taxes and transaction costs, while maximizing the estimated value of your stock portfolio next year. We will formulate this problem as a linear optimization problem.

You would like to sell enough shares of stock to generate $10,000 to use as part of a down payment on a new home. You need to decide how many shares of which stocks to sell in order to generate $10,000, after taxes and transaction costs, while maximizing the estimated value of your stock portfolio next year We will formulate this problem as a linear optimization problem.

What you will build

You will use Scipy to build equations and inequalities for a sequence of optimization problems to maximize the investor's profit under disparate conditions. If you have not heard linear optimization, you may want to read this before starting your project.

What you will learn

• Describe the optimization problems mathematically
• Build an equation with constraints
• Use Scipy to solve the problem
• Create an investment strategy based on the solutions

Check the package you need

• scipy

1. Describe the decision variables for this problem. How many are there?

There are 8 decision variables defined as xi, for i = 1,2,..., 8. xi represents the amount of shares of the i-th stock you want to sell.

2. We will assume for this problem that you can not sell more shares of stock than you own, and you can not buy additional shares. How should you constrain the values of the decision variables to account for this?

Since you have 150 shares of each stock at first, the constraint condition of the decision variables are as follows:

0≤xi≤150, i=1,2,⋯,8

3. Your objective is to maximize the estimated value of your stock portfolio next year. To do this, you should sum the estimated value of each stock next year. Suppose you sell x shares of your stock in Microsoft. What is the estimated value of your Microsoft stock next year?

Use the Microsoft's next year estimate price (34.55), which is multiplied by the remaining shares you hold after selling. The result is 34.55×(150−x).

4. Write out the objective function of this problem in terms of your decision variables.

Your aim is to maximize the remaining profit of the 8 different stocks next year. You should have the estimated stock price for each stock, multiplied by each remaining share, and then sum up. Following this idea, your objective function should be:

f(x1,x2,x3,x4,x5,x6,x7,x8)

=29.50∗(150−x1)+26.32∗(150−x2)+34.55∗(150−x3)+15.23∗(150−x4)+

62.43∗(150−x5)+26.68∗(150−x6)+23.85∗(150−x7)+31.66∗(150−x8)

After simplifying it, we can have:

f(x1,x2,x3,x4,x5,x6,x7,x8)

=37471.5−(29.50∗x1+26.31∗x2+34.55∗x3+15.23∗x4+

62.43∗x5+26.68∗x6+23.85∗x7+31.66∗x8)

5. In addition to the upper and lower bounds on your decision variables, you need to add one constraint to your model to make sure you get $ 10,000 in cash from selling your stocks, after taxes and transaction costs. Write down this constraint in terms of your decision variables.

The constraint is a little bit complicated because of the taxes and transaction costs. You should first exclude 1% of the amount transacted (hence 99% of the amount remains) and then minus 30% of the capital-gains. (Go through the ‘Description of the problem' part if you don't understand capital-gains.)

0.99∗(31.80∗x1+24.28∗x2+32.50∗x3+14.16∗x4+50.99∗x5+24.17∗x6+23.67∗x7+28.77∗x8)−0.3∗((31.80−15.68)∗x1+(24.28−22.10)∗x2+(32.50−30.39)∗x3+(14.16−8.93)∗x4+(50.99−40.55)∗x5+(24.17−18.58)∗x6+(23.67−22.54)∗x7+(28.77−24.84)∗x8)>10000

After simplifying it, we can have:

26.646∗x1+23.383∗x2+31.542∗x3+12.449∗x4+47.348∗x5+22.251∗x6+23.094∗x7+27.303∗x8>10000

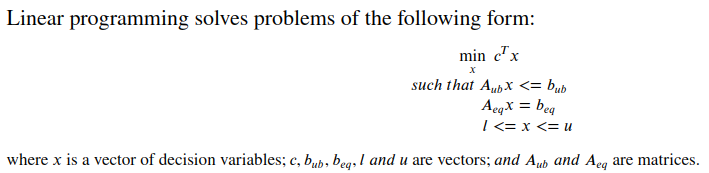
Set up and solve this problem in the optimization software you are using. Make sure you maximize your objective, including a constraint for the amount of cash you generate, and upper and lower bounds for the values of your decision variables.

1. What is the optimal solution? Give the values of the decision variables and the objective function value.

Maximizing the objective function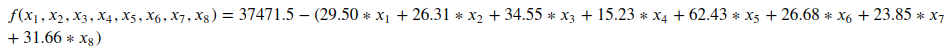

Is equivalent to minimizing the function below:

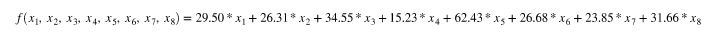
2. As an investor who is seeking to have a diverse portfolio, are you happy with this solution? Why or why not?

Optimal values of each xi yield:

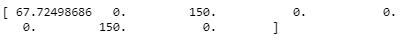
The investor would not be happy with this solution because those numbers show an unbalanced portfolio. The solution suggests the investor should have around 67 Yahoo! and sell all the stocks of Microsoft and Intel stocks. In addition, 0 means not sell any stocks.

Suppose you would like to keep at least 75 shares of each of your eight stocks. Adjust the formulation so that you sell no more than 75 shares of each stock, and solve the problem again.

What type of investor might prefer this solution over the previous one? What type of investor might prefer the previous solution over this one?

Optimal values of each xi yield:

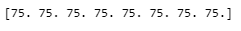
If an investor focuses on creating a diverse portfolio and does not care about the estimated profits next year, he or she would prefer taking this new solution. However, if the investor focuses on the estimated profit next year, he or she would take the previous solution.

Bertsimas.D, O'Hair.A.K, Pulleyblank.W.R(2016) The Analytics Edge. Chapter 22.6