Description of the problem
Time series are an essential part of financial analysis, Today, you have more data at your disposal than ever, more sources of data, and more frequent delivery of that data. New sources include new exchanges, social media outlets, and new sources. The frequency of delivery has increased from tens of messages per second 10 years ago, to hundreds of thousands of messages per second today. Naturally, more and different analysis techniques are being brought to bear as a result. Most of the modern analysis techniques aren't different in the sense of being new, and they all have their basis in statistics, but their applicability has closely followed the amount of computing power available. The growth in available computing power is faster than the growth in time series volumes, so it is possible to analyze time series today at scale in ways that weren't previously practical.
In particular, machine learning techniques, especially deep learning, hold great promise for time series analysis. As time series become more dense and many time series overlap, machine learning offers a way to separate the signal from the noise, even when the noise can seem overwhelming. Deep learning holds great potential because it is often the best fit for the seemingly random nature of financial time series.
The premise
Financial markets are increasingly global, and if you follow the sun from Asia to Europe to the US and so on, you can use information from an earlier time zone to your advantage in a later time zone. The following table shows a number of stock market indices from around the globe, their closing times in Eastern Standard Time (EST), and the delay in hours between the close that index and the close of the S&P 500 in New York. This makes EST the base time zone. For example, Australian markets close for the day 15 hours before US markets close. If the close of the All Ords in Australia is a useful predictor of the close of the S&P 500 for a given day we can use that information to guide our trading activity. Continuing our example of the Australian All Ords, if this index closes up and we think that means the S&P 500 will close up as well then we should either buy stocks that composes the S&P 500 or, more likely, an ETF that tracks the S&P 500. In reality, the situation is more complex because there are commissions and tax to account for. But as a first approximation, we'll assume an index closing up indicates a gain, an vice-versa.
Index | Country | Closing Time (EST) | Hours Before S&P Close |
All Ords | Australia | 0100 | 15 |
Nikkei 225 | Japan | 0200 | 14 |
Hang Seng | Hong Kong | 0400 | 12 |
DAX | Germany | 1130 | 4.5 |
FTSE 100 | UK | 1130 | 4.5 |
NYSE Composite | US | 1600 | 0 |
Dow Jones Industrial Average | US | 1600 | 0 |
S&P 500 | US | 1600 | 0 |
What you will build
- Binary classification with TensorFlow
- Logistic regression classifier, random forest classifier, gradient boosting classifier and multi-layer perceptron classifier with sklearn
What you will learn
- Obtain data for a number of financial markets.
- Perform exploratory data analysis in order to explore and validate a premise.
- Use TensorFlow and sklearn to build, train and evaluate a number of models for predicting what will happen in financial markets
- pandas
- numpy
- matplotlib
- tensorflow
- sklearn
In this project, you can use the dataset in "closing_data.csv" in Qusandbox directly. Or you can also retrieve the data using BigQuery API in your local jupyter notebook.
The data covers roughly the last 5 years, using the date range from 1/1/2010 to 10/1/2015. Data comes from the S&P 500 (S&P), NYSE, Dow Jones Industrial Average (DJIA), Nikkei 225 (Nikkei), Hang Seng, FTSE 100 (FTSE), DAX, and All Ordinaries (AORD) indices.
The closing prices are of interest, so for convenience extract the closing prices for each of the indices into a single Pandas DataFrame, called closing_data. Because not all of the indices have the same number of values, mainly due to bank holidays, we'll forward-fill tha gaps. This means that, if a value isn't available for day N, fill it with the value for another day, such as N-1 or N-2, so that it contains the latest available value.
At this point, you've sourced five years of time series for eight financial indices, combined the pertinent data into a single data structure, and harmonized the data to have the same number of entries, by using only 20 lines of code (commented) in the notebook.
Exploratory Data Analysis (EDA) is foundational to working with machine learning, and any other sort of analysis. EDA means getting to know your data, getting your fingers dirty with your data, feeling it and seeing it. The end result is you know your data very well, so when you build models you build them based on an actual, practical, physical understanding of the data, not assumptions or vaguely held notions. You can still make assumptions of course, but EDA means you will understand your assumptions and why you're making those assumptions.
First, take a look at the data.
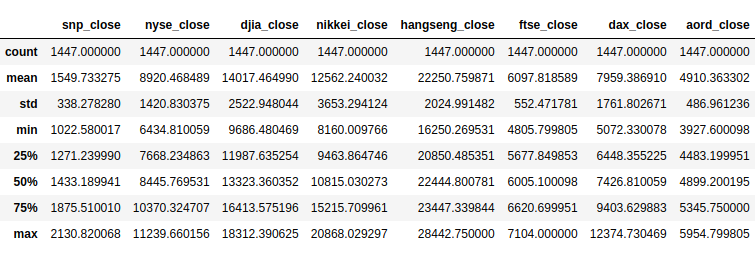
You can see that the various indices operate on scales differing by orders of magnitude. It's best to scale the data so that, for example, operations involving multiple indices aren't unduly influenced by a single, massive index.
Actual value EDA
The original data plot should be like this:
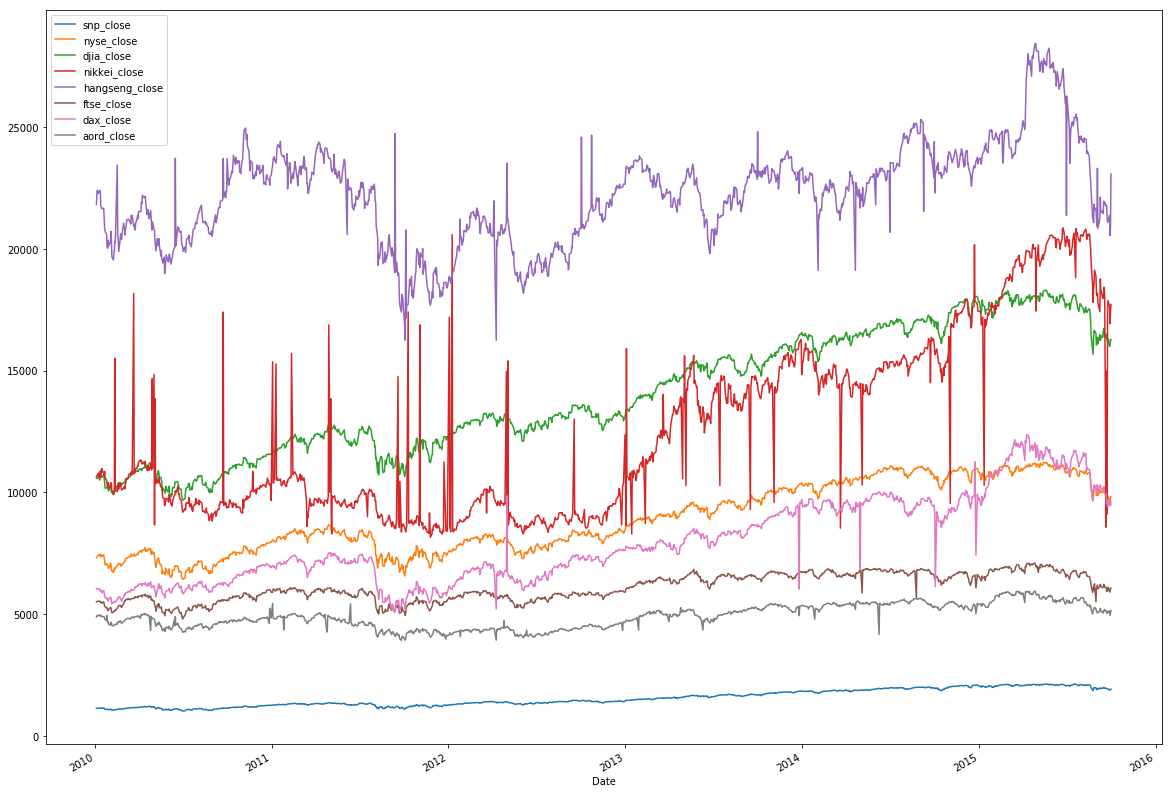
As expected, the structure isn't uniformly visible for the indices. Divide each value in an individual index by the maximum value for that index, and then replot. The maximum value of all indices will be 1.
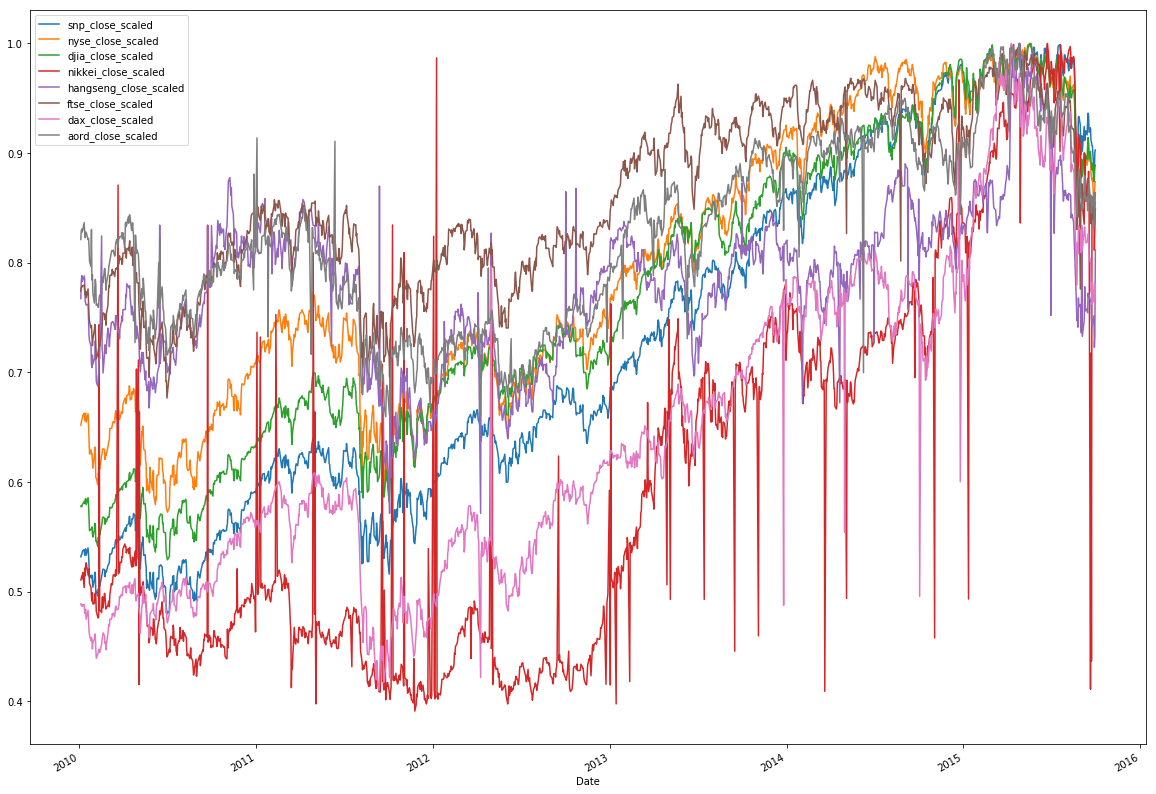
Now, you can see that, over the five-year period, these indices are correlated. Notice that sudden drops from economic events happened globally to all indices, and they otherwise exhibited general rises. This is an good start, though not the complete story.
Next, plot autocorrelations for each of the indices. The autocorrelations determine correlations between current values of the index and lagged values of the same index. The goal is to determine whether the lagged values are reliable indicators of the current values. If they are, then we've identified a correlation.
The plot should be like this:
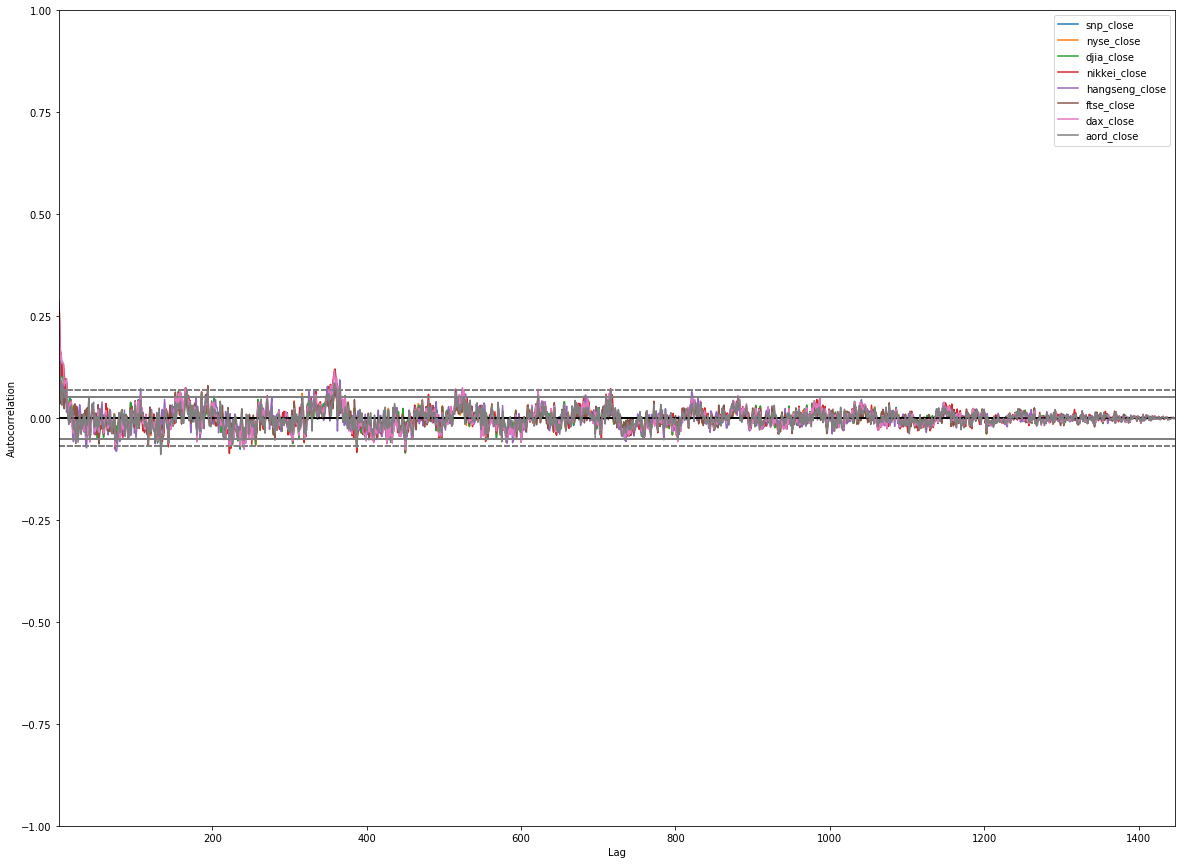
You should see strong autocorrelations, positive for around 500 lagged days, then going negative. This tells us something we should intuitively know: if an index is rising it tends to carry on rising, and vice-versa. It should be encouraging that what we see here conforms to what we know about financial markets.
Next, look at a scatter matrix, showing everything plotted against everything, to see how indices are correlated with each other.
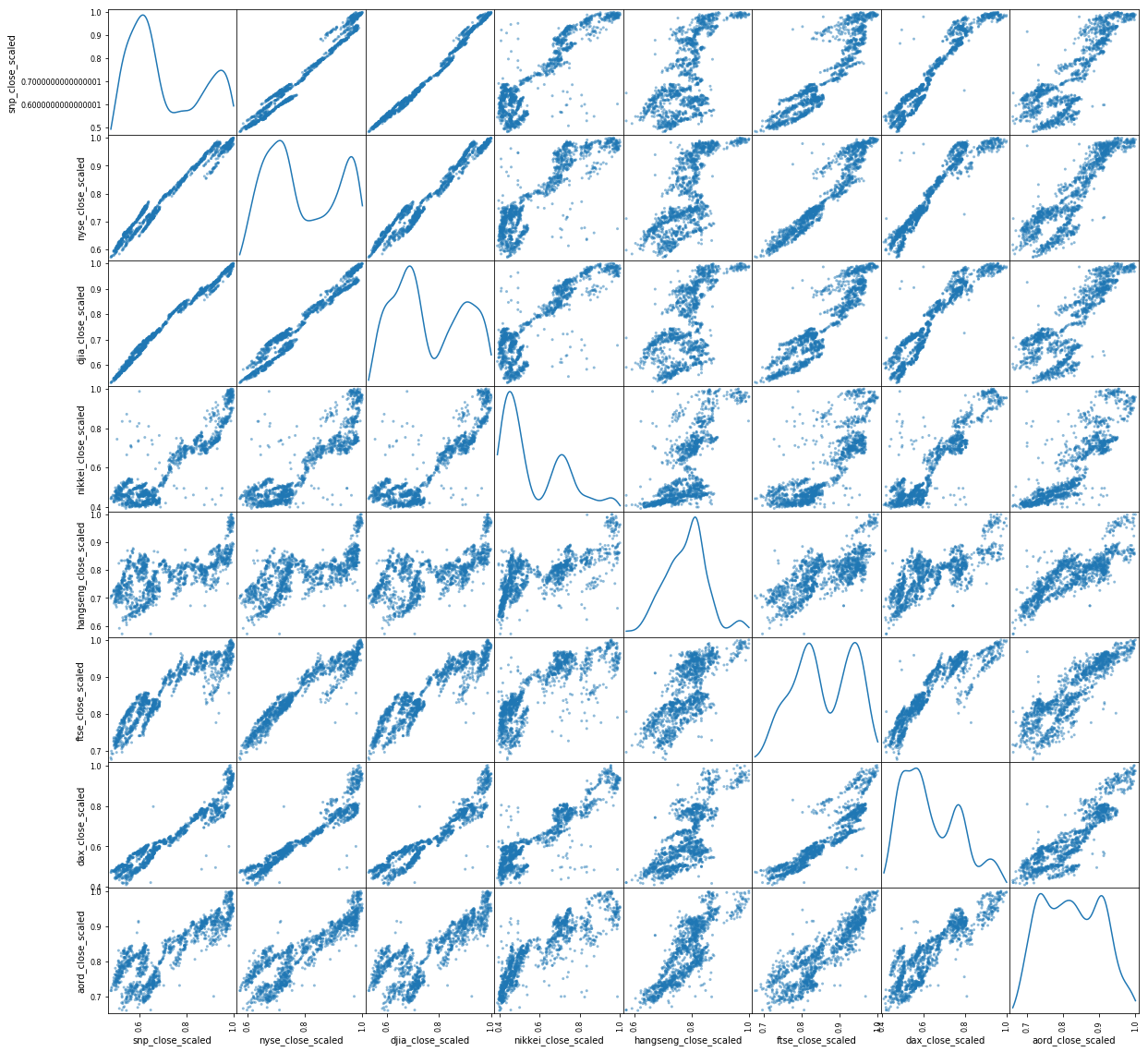
You can see significant correlations across the board, further evidence that the premise is workable and one market can be influenced by another.
As an aside, this process of gradual, incremental experimentation and progress is the best approach and what you probably do normally. With a little patience, we will get to some deeper understanding.
Log returns EDA
The actual value of an index is not that useful for modeling. It can be a useful indicator, but to get to the heart of the matter, we need a time series that is stationary in the mean, thus having no trend in the data. There are various ways of doing that, but they all essentially look at the difference between values, rather than the absolute value.
In this case of market data, the usual practice is to work with logged returns, calculated as the natural logarithm of the index today divided by the index yesterday:
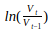
There are more reasons why the log return is preferable to the percent return (for example the log is normally distributed and additive), but they don't matter much for this work. What matters is to get to a stationary time series.
So one more thing you need to do is to calculate and plot the log returns in a new DataFrame.
The description of the new data is shown below:
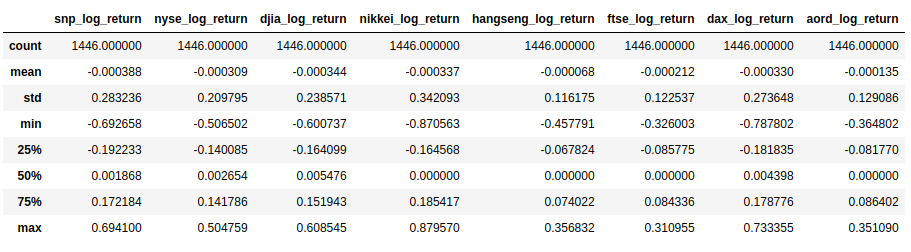
Looking at the log returns, you should see that the mean, min, max are all similar. You should go further and center the series on zero, scale them, and normalize the standard deviation, but there's no need to do that at this point. Let's move forward with plotting the data, and iterate if necessary.
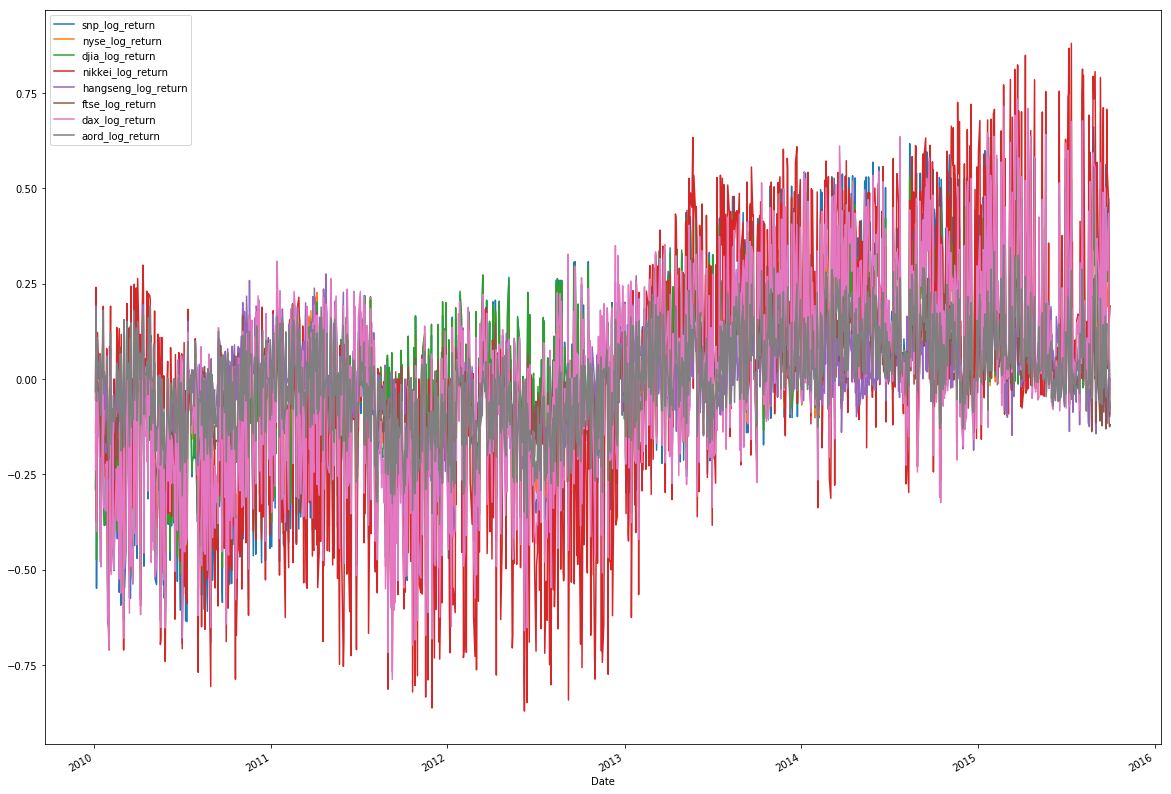
From the new plot, you can see that the log returns of our indices are similarly scaled and centered, with no visible trend in the data. It's looking good, so now look at autocorrelations:

No autocorrelations are visible in the plot, which is what we're looking for. Individual financial markets are Markov processes, knowledge of history doesn't allow you to predict the future.
You now have time series for the indices, stationary in the mean, similarly centered and scaled. That's great! Now start to look for signals to try to predict the close of the S&P 500.
Look at a scatterplot to see how the log return indices correlate with each other:
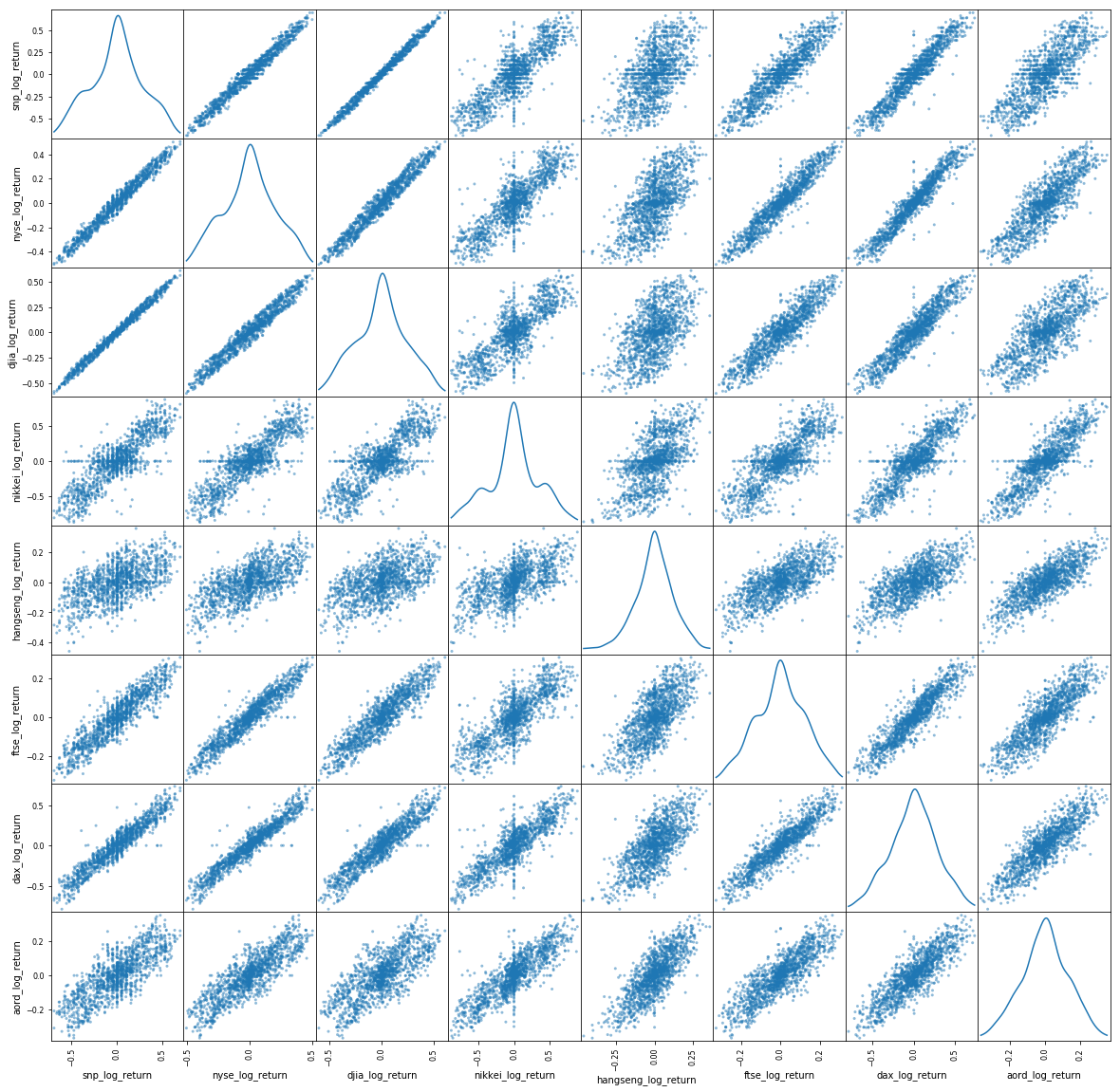
The story with the previous scatter plot for log returns is more subtle and more interesting. The US indices are strongly correlated, as expected. The other indices, less so, with is also expected. But there is structure and signal there. Now let's move forward and start to quantify it so we can start to choose features for our model.
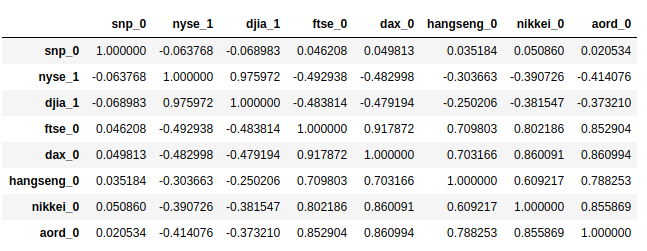
First look at how the log returns for the closing value of the S&P 500 correlate with the closing values of other indices available on the same day. This essentially means to assume the indices that close before the S&P 500 (non-US indices) are available and the others (US indices) are not.
The result shows below:

Here, we are directly working with the premise. We're correlating the close of the S&P 500 with signals available before the close of the S&P 500. And you see that the S&P 500 close is correlated with European indices at around 0.9 for the FTSE and DAX, which is a strong correlation, and Asian/Oceanian indices at around 0.5-0.8, which is a significant correlation, but not with US indices. We have available signals from other indices and regions for our model.
Now look at how the log returns for the S&P closing values correlate with index values from the previous day to see if they previous closing is predictive. Following from the premise that financial market are Markov processes, there should be little or no value in historical values.

You should see little to no correlation in this data, meaning that yesterday's values are no practical help in predicting today's close. Let's go one step further and look at correlations between today and the day before yesterday.

Again, there are little or no correlations.
Summing up the EDA
At this point you've done a good enough job of exploratory data analysis. You've visualized our data and come to know it better. You've transformed it into a form that is useful for modelling, log returns, and looked at how indices relate to each other. You've seen that indices from Europe strongly correlate with US indices, and that indices from Asia/Oceania significantly correlate with those same indices for a given day. You've also seen that if you look at historical values, they do not correlate with today's values.
Summing up:
- European indices from the same day were a strong predictor for the S&P 500 close.
- Asian/Oceanian indices from the same day were a significant predictor for the S&P 500 close.
- Indices from the previous days were not good predictors for the S&P close.
At this point, we can see a model:
- We'll predict whether the S&P 500 close today will be higher or lower than yesterday.
- We'll use all our data sources: NYSE, DJIA, Nikkei, Hang Seng, FTSE, DAX, AORD.
- We'll use three sets of data points-- T, T-1, and T-2 -- where we take the data available on day T or T-n, meaning today's non-US data and yesterday's US data.
Predicting whether the log return of the S&P 500 is positive or negative is a classification problem. That is, we want to choose one option from a finite set of options, in this case positive or negative. This is the base case of classification, where we have only two values to choose from, known as binary classification, or logistic regression.
This uses the findings from of our exploratory data analysis (Step 3), namely that log returns from other regions on a given day are strongly correlated with the log return of the S&P 500, and there are stronger correlations from those regions that are geographically closer with respect to time zones. However, our models also use data outside of those findings. For example, we use data from the past few days in addition to today. THere are two reasons for using this additional data. First, we're adding additional features to our model for the purpose of this solution to see how things perform, which is not a good reason to add features outside of a tutorial setting. Second, machine learning models are very good at finding weak signals from data.
In machine learning, as in most things, there are subtle tradeoffs happening, but in general good data is better than good algorithms, which are better than good frameworks. You need all three pillars but in that order of importance: data, algorithms, frameworks.
TensorFlow is an open source software library, initiated by Google, for numerical computation using data flow graphs. TensorFlow is based on Google's machine learning expertise and is the next generation framework used internally at Google for tasks such as translation and image recognition. It's a wonderful framework for machine learning because it's expressive, efficient, and easy to use.
Feature engineering for TensorFlow
From a training and testing perspective, time series data is easy. Training data should come from events that happened before test data events, and be contiguous in time. Otherwise, your model would be trained on events from "the future", at least as compared to the test data. It would then likely perform badly in practice, because you can't really have access to data from the future. That means random sampling or cross validation don't apply to time series data. Decide on a training-versus-testing split, and divide your data into training and test dataset.
In this case, you'll create the features together with two additional columns:
- snp_log_return_positive, which is 1 if the log return of the S&P 500 close is positive, and 0 otherwise.
- snp_log_return_negative, which is 1 if the log return of the S&P 500 close is negative, and 0 otherwise.
Now, logically you could encode this information in one column, named snp_log_return, which is 1 if positive and 0 if negative, but that's not the way TensorFlow works for classification models. TensorFlow uses the general definition of classification, that there can be many different potential values to choose from, and a form or encoding for these options called one-hot encoding. One-hot encoding means that each choice is an entry in an array, and the actual value has an entry of 1 with all other values being 0. This encoding (i.e. a single 1 in an array of 0s) is for the input of the model, where you categorically know which value is correct. A variation of this is used for the output, where each entry in the array contains the probability of the answer being that choice. You can then choose the most likely value by choosing the highest probability, together with having a measure of the confidence you can place in that answer relative to other answers.
We'll use 80% of our data for training and 20% for testing.
Implement the TensorFlow model
Now, get some tensors flowing. The model is binary classification expressed in TensorFlow.
Steps to define our TensorFlow model:
- Define placeholders for the data we feed into the process -- feature data and actual classes.
- Define a matrix of weights and initialize it with some small random values.
- Take a softmax regression of the product of our feature data and weights.
- Define a cost function (we're using the cross entropy)
- Define a training step: use gradient descent with a learning rate of 0.01 using the cost function we just defined.
We'll train our model in the following snippet. The approach of TensorFlow to executing graph operations allows fine-grained control over the process. Any operation you provide to the session as part of the run operation will be executed and the results returned. You can provide a list of multiple operations.
You'll train the model over 30,000 iterations using the full dataset each time. Every thousandth iteration we'll assess the accuracy of the model on the training data to assess progress.
Evaluate the model
You can also define some metrics to evaluate the models in TensorFlow.
- Precision: The ability of the classifier not to label as positive a sample that is negative.
- Recall: The ability of the classifier to find all the positive samples.
- F1 score: A weighted average of the precision and recall, where an F1 score reaches its best value at 1 and worst score at 0.
- Accuracy: The percentage correctly predicted in the test data.
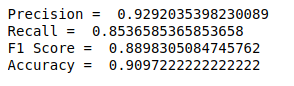
The performance of this model is shown below:

This model should have better performance since its simplicity and it hasn't been tuned. Selection of hyperparameters is very important in machine learning modeling.
Now you'll build a proper feed-forward neural net with two hidden layer.
Again, you'll train the model over 30,000 iterations using the full dataset each time. Every thousandth iteration, you'll assess the accuracy of the model on the training data to assess progress.
From the result, you we'll see a significant improvement in accuracy with the training data shows that the hidden layers are adding additional capacity for learning to the model.
Looking at precision, recall, and accuracy, you can see a measurable improvement in performance, but certainly not a step function. This indicates that we're likely reaching the limits of this relatively simple feature set.
Scikit-learn is also one of the best libraries to build Machine learning applications with. It is ideal for beginners because it has a really simple interface, it is well documented with many examples and tutorials.
Besides supervised machine learning (classification and regression), it can also be used for clustering, dimensionality reduction, feature extraction and engineering, and pre-processing the data. The interface is consistent over all of these methods, so it is not only easy to use, but it is also easy to construct a large ensemble of classifiers/regression models and train them with the same commands.
In next few step, we are going to learn how to build, train, evaluate and validate a classifier with scikit-learn, improve upon the initial classifier with hyper-parameter optimization. The classifiers we'll use are a logistic regression model, a Random forest classifier, a Gradient Boosting classifier and a multi-layer perceptron classifier.
Feature engineering for sklearn
In sklearn, we don't need two classes as the target for prediction but only one called snp_log_return_positive, which is 1 if positive and 0 if negative. We'll also use 80% of our data for training and 20% for testing.
Tuning the hyperparameter
Hyperparameters is like the settings of an algorithm that can be adjusted to optimize performance. Sklearn implements a set of sensible default hyperparameters for all models, but these are not guaranteed to be optimal for a problem. The best hyperparameters are usually impossible to determine ahead of time, and tuning a model is where machine learning turns from a science into trial-and-error based engineering. Usually, the standard procedure for hyperparameter optimization accounts for overfitting through cross validation. But for time-series dataset, we cannot use cross validation but split the train set into training and validation set for tuning to find the best hyperparameter.
Evaluate the model
The sklearn.metrics module implements several loss, score and utility function to measure classification performance. Some metrics might require probability estimates of the positive class, confidence values, or binary decisions values.
In this project, we use following metrics:
- accuracy_score: Accuracy classification score.
- classification_report: build a text report showing the main classification metrics
- precision_score: Compute the precision
- recall_score: Compute the recall
- f1_score: Compute the F1 score, also known as balanced F-score or F-measure
- roc_curve: Compute Receiver operating characteristic (ROC)
- roc_auc_score: Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores.
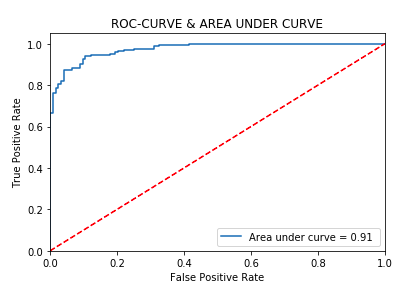
Hyperparameter Tuning | Best score | 0.93 | |
Best penalty | l1 | Best C | 1.68 |
Modeling | |||
Accuracy score | 0.92 | Precision score | 0.92 |
Recall score | 0.92 | F1-score | 0.92 |
AUC | 0.91 |
Hyperparameter Tuning | Best score | 0.95 | |
Best max_features | 7 | Best max_depth | None |
Best min_samples_split | 9 | Best bootstrap | False |
Best min_samples_leaf | 3 | ||
Modeling | |||
Accuracy score | 0.92 | Precision score | 0.92 |
Recall score | 0.92 | F1-score | 0.92 |
AUC | 0.92 |
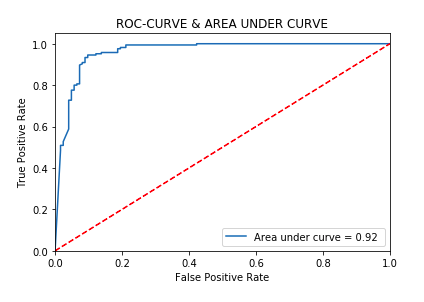
Hyperparameter Tuning | Best score | 0.94 | |
Best max_features | 15 | Best max_depth | 4 |
Best n_estimators | 60 | ||
Modeling | |||
Accuracy score | 0.91 | Precision score | 0.91 |
Recall score | 0.91 | F1-score | 0.91 |
AUC | 0.91 |
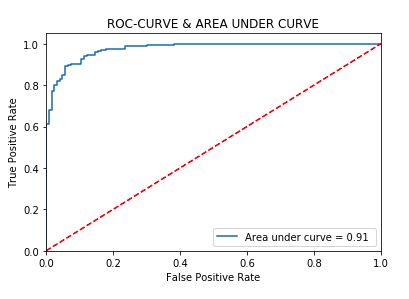
Hyperparameter Tuning | Best score | 0.94 | |
Best solver | lbfgs | Best activation | relu |
Best learning_rate | constant | Best hidden_layer_sizes | 6 |
Modeling | |||
Accuracy score | 0.91 | Precision score | 0.91 |
Recall score | 0.91 | F1-score | 0.91 |
AUC | 0.91 |
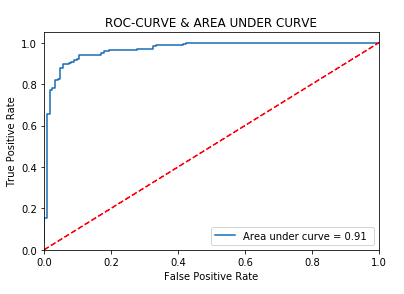
You've covered a lot of ground. You moved from sourcing five years of financial time-series data, to munging that data into a more suitable form. You explored and visualized that data with exploratory data analysis and then decided on machine learning models and the features for the model. You engineered those features, built a binary classifier and a feed forward neural net with two hidden layers in TensorFlow, a Logistic regression model, a Random forest classifier, a Gradient Boosting classifier and a multi-layer perceptron classifier in sklearn, and analyzed their performance.
How did we do with the data analysis? We did well: over 90% accuracy in predicting the close of the S&P 500 is the highest we've seen achieved on this dataset, so with few steps and a few lines of code we've produced a full-on machine learning model. The reason for the relatively modest accuracy achieved is the dataset itself; there isn't enough signal there to do significantly better. But 9 times out of 10, we were able to correctly determine if the S&P 500 index would close up or down on the day, and that's objectively good.
Result table
