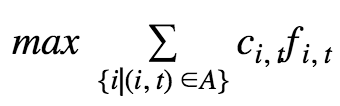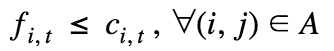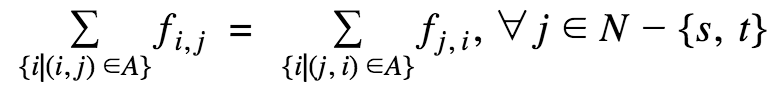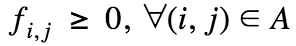Summary
The goal of the maximum flow problem is to find the maximum flow possible in a network from some given source nodes. Applications of the max flow problem include finding the maximum flow of orders through a job shop, the maximum flow of water through a storm sewer system, and the maximum flow of product through a product distribution system, among others, Schrijver (2002) note that the maximum flow problem was first formulated in 1954 by T. E. Harris and F. S. Ross as a simplified model of Soviet railway traffic flow.
A network is a directed graph, and the arc capacities, or upper bounds, are the only relevant parameters. A network graph does not have to be symmetric: if an arc (v, w) is in the graph, the reverse arc (w, v) does not have to be in the graph. Further, parallel arcs are not allows, an self-loops are not allowed. The source and the sink are distinct nodes in the network, but the sink may be unreachable from the source.
Problem Statement
The max flow problem can be formulated mathematically as a linear programming problem using the following model:
Sets | Set data that is used to define a model instance.
|
Parameters (Param) | Parameter data that is used to define a model instance.
|
Variables (Var) | Decision variables in a model.
|
Objective | Expressions that are minimized or maximized in a model.
|
Constraints | Constraint expressions that impose restrictions on variable values in a model.
|
- pyomo
First, you need to declare an abstract model by creating a model object. The AbstractModel class provides a context for defining and initializing abstract optimization models in Pyomo when the data values will be supplied at the time a solution is to be obtained.
model = AbstractModel()Then, use Set component to declare the sets N and A abstractly. When working with Pyomo, it is convenient to write abstract models in a somewhat more abstract way by using index sets that contain strings rather than index sets that are implied by 1, ..., m or the summation from 1 to n.
# Nodes in the network
model.N = Set()
# Network arc
model.A = Set(within=model.N*model.N)Similarly, the model parameters are defined abstractly using the Param component. The within option is used in these parameter declarations to define expected properties of the parameters. This information is used to perform error checks on the data that is used to initialize the parameter components.
For example, declare the "Source node" parameter:
model.s = Param(within=model.N)Use the Var component to define the decision variables, which in this case is the flow over each arc. The within option is used to restrict the domain of the decision variables to the non-negative reals. This eliminates the need for explicit bound constraints for variables.
# The flow over each arc
model.f = Var(model.A, within=NonNegativeReals)The Objective component is used to define the cost objective. This component uses a rule function to construct the objective expression
# Maximize the flow into the sink nodes
def total_rule(model):
return sum(model.f[i,j] for (i,j) in model.A if j==value(model.t)
model.total = Objective(rule=total_rule, sense=maximize)Similarly, rule functions are used to define constraint expressions in the Constraint component.
Finally, put these declarations all together and you will get your Pyomo model.
Since this is an abstract Pyomo model, the set and parameter values need to be provided to initialize the model. You can have a look at this synthetic data set:

Set data is defined with the set command, and parameter data is defined with the param command.
This data set considers the problem of maximizing flow in a zoo. A panda is about to give birth at the zoo! Officials anticipate that attendance will skyrocket to see the new, adorable baby panda. There's one particular residential area called "home" that is full of panda loving families and there's a fear that the increased number of people visiting the zoo will overload the public transportation system. It will be especially bad in the evening since the zoo closes about the same time as rush hour, so everyone will be trying to find space on the already crowded buses and subways. As a city planner, you were given a map of routes from the zoo to Home, along with the estimated number of families that could go on each route.Additionally, it was estimated that 16 families from Home will visit each day, and it's your task to figure out if this will overload the public transportation system, and, if it does, how could the system be improved?
Pyomo includes a pyomo command that automates the construction and optimization of models. The GLPK solver can be used in this simple example:
!pyomo solve --solver=glpk maxflow.py maxflow.datThis yields the following output on the screen:

The numbers in square brackets indicate how much time was required for each step. Results are written to the file named results.yml, which as a special structure that makes it useful for post-processing.
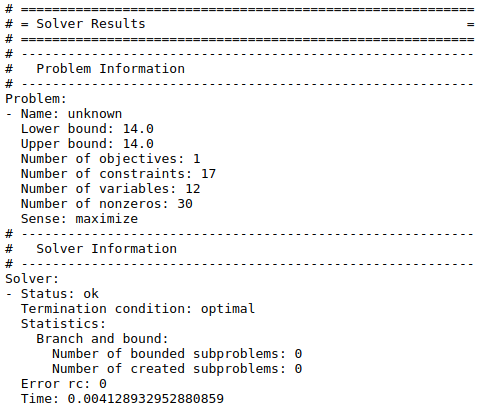
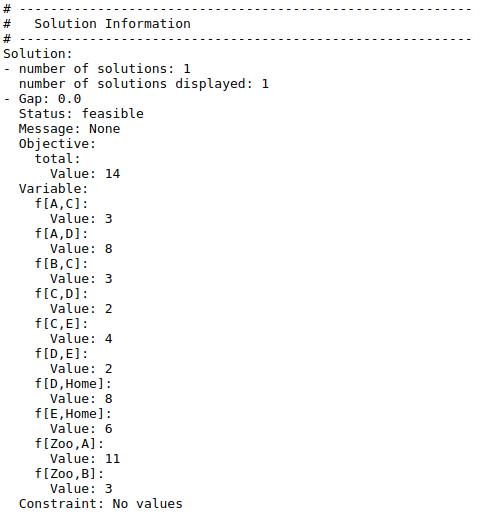
The output tells us how many people should travel along each route for the optimal solution. More importantly, though, is the line which says our objective value is 14. This means that at most 14 families can arrive at Home. However, we were told 16 families from Home were expected to visit the zoo each day. Therefore, unless something is done, the public transportation network in place will be overloaded.
- A. Schrijver, (2002). "On the history of the transportation and maximum flow problems". Mathematical Programming 91 (3): 437–445.