Summary

The goal of the Diet Problem is to select foods that satisfy daily nutritional requirements at minimum cost. This problem can be formulated as a linear program, for which constraints limit the number of calories and the amount of vitamins, minerals, fats, sodium, and cholesterol in the diet. Danzig (1990) notes that the diet problem was motivated by the US Army's desire to minimize the cost of feeding Gls in the field while stilling providing a healthy diet.

Problem Statement

The Diet Problem can be formulated mathematically as a linear programming problem using the following model in Pyomo:

Sets

Set data that is used to define a model instance.

  • F = set of foods
  • N = set of nutrients

Parameters (Param)

Parameter data that is used to define a model instance.

  • ci = cost per serving of food i, ∀i∈F
  • aij = amount of nutrient j in food i, ∀i∈F,∀j∈N
  • Nminj = minimum level of nutrient j, ∀j∈N
  • Nmaxj = maximum level of nutrient j, ∀j∈N
  • Vi = the volume per serving of food i, ∀i∈F
  • Vmax = maximum volume of food consumed

Variables (Var)

Decision variables in a model.

  • xi = number of servings of food i to consume

Objective

Expressions that are minimized or maximized in a model.

  • Minimize the total cost of the food
  • min∑i∈F cixi

Constraints

Constraint expressions that impose restrictions on variable values in a model.

  • Limit nutrient consumption for each nutrient j∈N
  • Nminj ≤ ∑i∈F (aijxi) ≤ Nmaxj, ∀j∈N
  • Limit the volume of food consumed
  • ∑i∈F Vixi ≤ Vmax
  • Consumption lower bound
  • xi ≥ 0, ∀i∈F

First, you need to declare an abstract model by creating a model object. The AbstractModel class provides a context for defining and initializing abstract optimization models in Pyomo when the data values will be supplied at the time a solution is to be obtained.

model = AbstractModel()

Then, use Set component to declare the sets F and N abstractly. When working with Pyomo, it is convenient to write abstract models in a somewhat more abstract way by using index sets that contain strings rather than index sets that are implied by 1, ..., m or the summation from 1 to n.

# Foods
model.F = Set()
# Nutrients 
model.N = Set()

Similarly, the model parameters are defined abstractly using the Param component. The within option is used in these parameter declarations to define expected properties of the parameters. This information is used to perform error checks on the data that is used to initialize the parameter components.

For example, declare the "cost of each food" parameter:

model.c = Param(model.F, within=PositiveReals)

Use the Var component to define the decision variables, which in this case is the number of servings consumed of each food. The within option is used to restrict the domain of the decision variables to the non-negative reals. This eliminates the need for explicit bound constraints for variables.

# Number of servings consumed of each food
model.x = Var(model.F, within=NonNegativeIntegers)

The Objective component is used to define the cost objective. This component uses a rule function to construct the objective expression

# Minimize the cost of food that is consumed
def cost_rule(model):
    return sum(model.c[i]*model.x[i] for i in model.F)
model.cost = Objective(rule=cost_rule)

Similarly, rule functions are used to define constraint expressions in the Constraint component.

Finally, put these declarations all together and you will get your Pyomo model.

Since this is an abstract Pyomo model, the set and parameter values need to be provided to initialize the model. You can have a look at this synthetic data set:

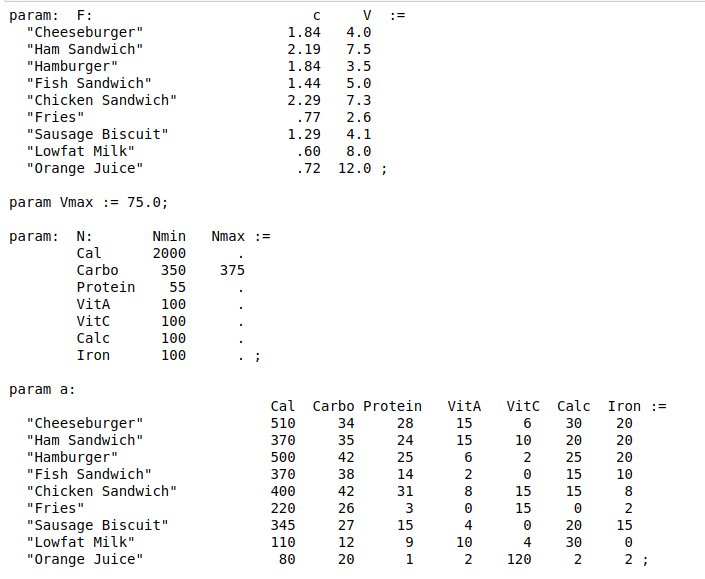
Set data is defined with the set command, and parameter data is defined with the param command.

This data set considers the problem of designing a daily diet with only food from a fast food chain.

Pyomo includes a pyomo command that automates the construction and optimization of models. The GLPK solver can be used in this simple example:

!pyomo solve --solver=glpk diet.py diet.dat

This yields the following output on the screen:

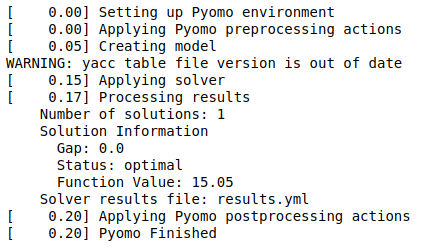
The numbers in square brackets indicate how much time was required for each step. Results are written to the file named results.yml, which as a special structure that makes it useful for post-processing.

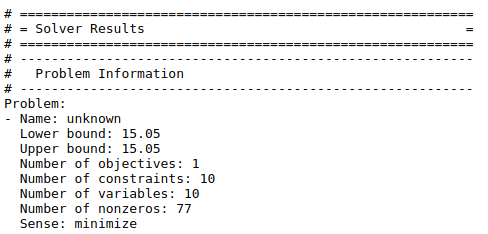
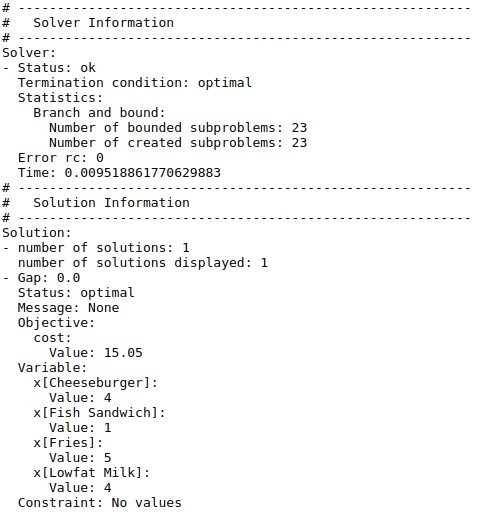
This solution shows that for about $15 per day, a person can get by with 4 cheeseburgers, 5 fries, 1 fish sandwich and 4 milks.