Description of the problem

In this project, you will build an AR(1) model using statsmodels and learn from the coefficient table to evaluate whether the series is a "random walk". The dataset you use is a time-series data of Walmart daily closing prices between February 2001 and February 2002 from textbook Data Mining For Business Analytics.

What you will build

What you will learn

In this project, you will learn how to:

First, use pd.read_excel (pandas) to read the excel file directly. After reading the dataset, you need to clean the data. In this dataset, there are several NaN values, which need to be replaced with 0. Use df.fillna(0).

Have a look of top 5 rows in the dataset:

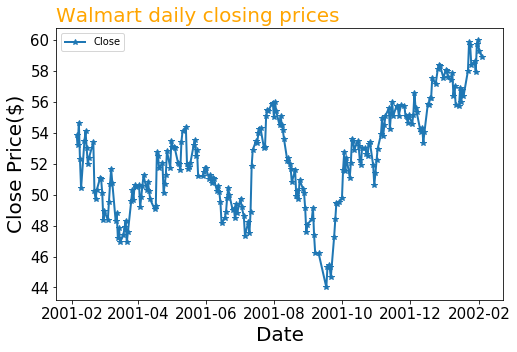
To visualize the time-series data, try plotting the data using matplotlib. You can also modify some attributes of figsize, marker, linewidth and fontsize to make your plot looks better.

First, extract the "Date" and "Close" columns from the dataframe to a new dataframe. Since it is a time-series data, it is important to set "Data" column as the index of the new dataframe.

Then, use this data to fit an AR(1) model using ARMA in statsmodels.

ARMA refers to Auto-regressive Moving Average model. An autoregression model makes an assumption that the observations at previous time steps are useful to predict the value at the next time step.

The order in the ARMA model is the (p, q) order of the model for the number of AR parameter differences, and MA parameters to use. Since we want to create an AR(1), which is an autoregressive model of order 1, you can set order=(1, 0). In other words, AR model is a special case of ARMA model, where order of MA is 0. Also, be aware that the AR model does not require the series being stationary. This means that we can use close_price variable as our target.

Aftering fitting the model, try summary() to see the coefficient table of the result.

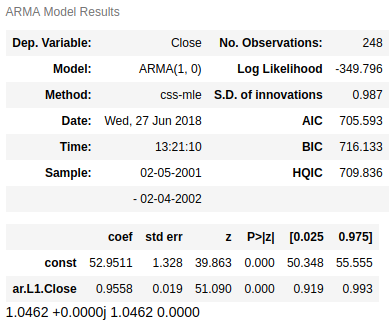
The AR(1) slope coefficient can evaluate whether a series is a random walk by testing the hypothesis that the slope coefficient is equal to 1. In this case, the slope coefficient in our model is 0.9558, with a standard error 0.019. With the coefficient being sufficiently close to 1 (around one standard error away), we can say that this is a random walk, namely unit root process. In other words, this makes the time series unpredictable. See unit root process for more math details on unit root problem. As we learned, the changes in the series from one period to the next are random, suggesting that its past cannot be used to predict its future.

Shmueli.G, Bruce.P.C, Patel.N.R (2016) Data Mining For Business Analytics (Third Edition)